Anonymous assets

DarkFi network allows for the issuance and transfer of anonymous assets with an arbitrary number of parameters. These tokens are anonymous, relying on zero-knowledge proofs to ensure validity without revealing any other information. All transactions over the network are managed by smart contracts.

New tokens are created and destroyed every time you send an anonymous transaction. To send a transaction on DarkFi, you must first issue a credential that commits to some value you have in your wallet. This is called the Mint phase. Once the credential is spent, it destroys itself: what is called the Burn.

Through this process, the link between inputs and outputs is broken.

Mint

During the Mint phase we create a new coin commitment $C$, which is bound to the public key $P$. The coin commitment $C$ is publicly revealed on the blockchain and added to the merkle tree, which is stored locally on the DarkFi wallet.

We do this using the following process:

Let $v$ be the coin's value. Generate random $r_C$, $r_V$ and a secret serial $\rho$. The random values ensure the uniqueness and security of the commitment; the serial $\rho$ will be later used to generate the nullifier $N$ of the burn phase and to tie $N$ to $C$.

Create a commitment to these parameters in zero-knowledge:

$$C=H(P,v,\rho ,r_C)$$

Check that the value commitment is constructed correctly:

$$v>0$$ $$V=v{G}_1+r_V{G}_2$$

Reveal $C$ and $V$ commitments. Add $C$ to the Merkle tree.

Burn

When we spend the coin, we must ensure that the value of the coin cannot be double spent. We call this the Burn phase. The process relies on a $N$ nullifier, which we create using the secret key $x$ for the public key $P$ and the coin itself $C$. Nullifiers are unique per coin and prevent double spending. $R$ is the Merkle root. $v$ is the coin's value.

Generate a random number $r_V$.

Check that the secret key corresponds to a public key:

$$P=xG$$

Check that the public key corresponds to a coin which is in the merkle tree $R$:

$$C=H(P,v,\rho ,r_C)$$ $$C\in R$$

Derive the nullifier:

$$N=H(x,C)$$

Check that the value commitment is constructed correctly:

$$v>0$$ $$V=v{G}_1+r_V{G}_2$$

Reveal $N$, $V$ and $R$. Check $R$ is a valid Merkle root. Check $N$ does not exist in the nullifier set.

The zero-knowledge proof confirms that $N$ binds to an unrevealed value $C$, and that this coin is in the Merkle tree, without linking $N$ to $C$. Once the nullifier is produced the coin becomes unspendable.

Adding values

Assets on DarkFi can have any number of values or attributes. This is achieved by creating a credential $C$ and hashing any number of values and checking that they are valid in zero-knowledge.

We check that the sum of the inputs equals the sum of the outputs. This means that:

$$B=\sum V_{in}-\sum V_{out}$$

And that $B$ is a valid point on the curve $G_2$.

This proves that $B=0G_1+b{G}_2=b{G}_2$ where $b$ is a secret blinding factor for the amounts.

Diagram

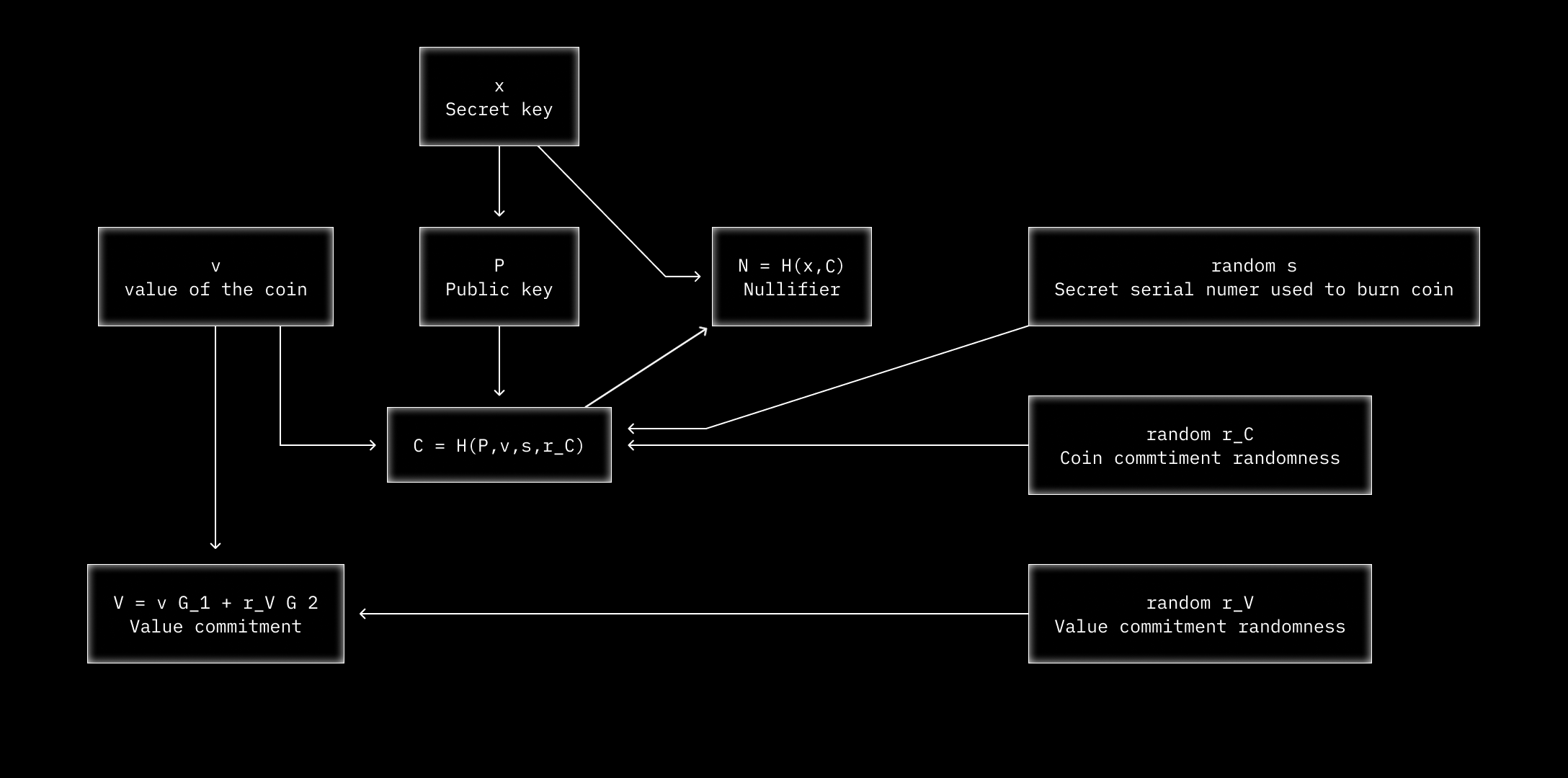
Note: In the diagram $s$ correspond to the $\rho$