DarkFi

About DarkFi

DarkFi is a new Layer 1 blockchain, designed with anonymity at the forefront. It offers flexible private primitives that can be wielded to create any kind of application. DarkFi aims to make anonymous engineering highly accessible to developers.

DarkFi uses advances in zero-knowledge cryptography and includes a contracting language and developer toolkits to create uncensorable code.

In the open air of a fully dark, anonymous system, cryptocurrency has the potential to birth new technological concepts centered around sovereignty. This can be a creative, regenerative space - the dawn of a Dark Renaissance.

Connect to DarkFi IRC

Follow the installation instructions for the P2P IRC daemon.

Build

This project requires the Rust compiler to be installed. Please visit Rustup for instructions.

You have to install a native toolchain, which is set up during Rust installation, nightly toolchain and wasm32 target. To install nightly toolchain, execute:

% rustup toolchain install nightly

To install wasm32 target, execute:

% rustup target add wasm32-unknown-unknown
% rustup target add wasm32-unknown-unknown --toolchain nightly

Minimum Rust version supported is 1.77.0 (nightly).

The following dependencies are also required:

Users of Debian-based systems (e.g. Ubuntu) can simply run the following to install the required dependencies:

# apt-get update
# apt-get install -y git make gcc pkg-config libasound2-dev libssl-dev libsqlcipher-dev wabt

Alternatively, users can try using the automated script under contrib folder by executing:

% sh contrib/dependency_setup.sh

The script will try to recognize which system you are running, and install dependencies accordingly. In case it does not find your package manager, please consider adding support for it into the script and sending a patch.

To build the necessary binaries, we can just clone the repo, checkout to the latest tag, and use the provided Makefile to build the project:

% git clone https://github.com/darkrenaissance/darkfi
% cd darkfi && git checkout v0.4.1
% make

Development

If you want to hack on the source code, make sure to read some introductory advice in the DarkFi book.

Living on the cutting edge

Since the project uses the nightly toolchain, breaking changes are bound to happen from time to time. As a workaround, we can configure an older nightly version, which was known to work:

% rustup toolchain install nightly-2024-02-01
% rustup target add wasm32-unknown-unknown --toolchain nightly-2024-02-01

Now we can use that toolchain in make directly:

% make CARGO="cargo +nightly-2024-04-05" {target}

Or, if we are lazy, we can modify the Makefile to always use that:

% sed -i Makefile -e "s|nightly|nightly-2024-02-01|g"

Under no circumstances commit or push the Makefile change.

When using cargo directly, you have to add the +nightly-2024-02-01 flag, in order for it to use the older nightly version.

Install

This will install the binaries on your system (/usr/local by default). The configuration files for the binaries are bundled with the binaries and contain sane defaults. You'll have to run each daemon once in order for them to spawn a config file, which you can then review.

# make install

Examples and usage

See the DarkFi book

Go Dark

Let's liberate people from the claws of big tech and create the democratic paradigm of technology.

Self-defense is integral to any organism's survival and growth.

Power to the minuteman.

Start Here

Directory Structure

DarkFi broadly follows the standardized unix directory structure.

• All bundled applications are contained in bin/ subdirectory.
• Random scripts and helpers such as build artifacts, node deployment or syntax highlighting is in contrib/.
• Documentation is in doc/.
• Example codes are in example/.
• Script utilities are in script/. See also the large script/research/ subdir.
• All core code is contained in src/. See Architecture Overview for a detailed description.
  • The src/sdk/ crate is used by WASM contracts and core code. It contains essential primitives and code shared between them.
  • src/serial/ is a crate containing the binary serialization code, which is the same as used by Bitcoin.
  • src/contract/ contains our native bundled contracts. It's worth looking at these to familiarize yourself with what contracts on DarkFi are like.

Using DarkFi

Refer to the main README file for instructions on how to install Rust and necessary deps.

Then proceed to the Running a Node guide.

Join the Community

Although we have a Telegram, we don't believe in centralized proprietary apps, and our core community organizes through our own fully anonymous p2p chat system which has support for Nym and Tor.

Every Monday at 16:00 CET in #dev we have our main project meeting.

See the guide on darkirc for instructions on joining.

Contributing as a Dev

Check out the contributor's guide for where to find tasks and submitting patches to the project.

If you're not a dev but wish to learn then take a look at the agorism hackers study guide.

Lastly familiarize yourself with the project architecture. The book also contains a cryptography section with a helpful ZK explainer.

DarkFi also has a project spec and a DEP (Drk Enhancement Proposals) system.

Detailed Overview

Source code is under src/ subdirectory. Main interesting modules are:

• net/ is our own p2p network. There are sessions such as incoming or outgoing that have channels (connections). Protocols are attached to channels depending on the session. The p2p network is also multi-transport with support for TCP (+TLS), Tor and Nym. So you can access the p2p fully anonymously (network level privacy).
• event_graph/ which is a DAG sync protocol used for ensuring eventual consistency of data, such as with chat systems (you don't drop any messages).
• runtime/ is the WASM smart contract engine. We separate computation into several stages which is checks-effects-interactions paradigm in solidity but enforced in the smart contract explicitly. For example in the exec() phase, you can only read, whereas writes must occur in the apply(update) phase.
• blockchain/ and validator/ is the blockchain and consensus algos.
• zk/ is the ZK VM, which is simply loads bytecode which is used to build the circuits. It's a very simple model rather than the TinyRAM computation models. We opted for this because we prefer simplicity in systems design.
• sdk/ contains a crypto SDK usable in smart contracts and applications. There are also Python bindings here, useful for making utilities or small apps.
• serial/ contains our own serialization because we don't trust rust serialization libs like serde (recently confirmed when they start bundling binaries). We also have async serialization and deserialization which is good for network code.
• tx/ is the tx we use. Note signatures are not in the calldata as having this outside it allows more efficient verification (since you can do it in parallel and so on).
  • All darkfi calls are precomputed ahead of time which is needed for ZK. Normally in eth or other smart contract chains, the calldata is calculated where the function is invoked. Whereas in darkfi the entire callgraph and calldata is bundled since ZK proofs must be computed ahead of time. This also improves things like static analysis and security (limiting call depth is easy to check before verification).
  • Verifying sigs or call depth ahead of time helps make the chain more attack resistant.
• contract/ contains our native smart contracts. Namely:
  • money, which is multi-asset anonymous transfers, anonymous swaps and token issuance. The token issuance is programmatic. When creating a token, it commits to a smart contract which specifies how the token is allowed to be issued.
  • deploy for deploying smart contracts.
  • dao, which is a fully anonymous DAO. All the DAOs on chain are anonymous, including the amounts and activity of the treasury. All participants are anonymous, proposals are anonymous and votes are anonymous including the token weighted vote amount, and user identity. You cannot see who is in the DAO.

NOTE: we try to minimize external dependencies in our code as much as possible. We even try to limit dependencies within submodules.

Inside bin/ contains utilities and applications:

• darkfid/ is the daemon and drk/ is the wallet. Currently being updated to the new testnet (if you see the commit log last few days).
• dnet/ is a viewer to see the p2p traffic of nodes, and deg/ is a viewer for the event graph data. We use these as debugging and monitoring tools.
• dhtd/ is a distributed hash table, like IPFS, for transferring static data and large files around. Currently just a prototype but we'll use this later for images in the chat or other static content like seller pages on the marketplace.
• tau/ is an anon p2p task manager which we use. We don't use github issues, and seek to minimize our dependence on centralized services. Eventually we want to be fully p2p and attack resistant.
• darkirc/ is our main community chat. It uses RLN; you stake money and if you post twice in an epoch then you get slashed which prevents spam. There is a free tier. It uses the event_graph for synchronizing the history. You can attach any IRC frontend to use it rn. Later we'll make our own UI.
• zkas/ is our ZK compiler.
• zkrunner/ contains our ZK debugger (run zkrunner with --trace), and zkrender which renders a graphic of the circuit layout.
• lilith/ is a universal seed node. Eventually we will add swarming support to our p2p network which is an easy addon.

Lastly worth taking a look is script/research/ and script/research/zk/ which contains impls of most major ZK algos. bench/ contains benchmarks. script/escrow.sage is a utility for doing escrow. We'll integrate it in the wallet later, but it works for now.

We could say more on our design philosophy of simplicity oriented approach to systems dev, but I'll drop these links here for now:

• Suckless Philosophy: software that sucks less
• How to Design Perfect (Software) Products by Pieter Hintjens

Recent crypto code audit: ZK Security DarkFi Code Audit

Useful link on our ZK toolchain

For proof files, see proof/ and src/contract/*/proof/ subdirs.

DarkFi Philosophy

State Civilization and the Democratic Nation

State civilization has a 5000 year history. The origin of civilizations in mesopotamia experienced a cambrian explosion of various forms. The legacy of state civilization can be traced back to ancient assyria which was essentially a military dictatorship that mobilized all of society's resources to wage war and defeat other civilizations, enslaving them and seizing their wealth.

Wikipedia defines civilization:

Civilizations are organized densely-populated settlements divided into hierarchical social classes with a ruling elite and subordinate urban and rural populations.

Civilization concentrates power, extending human control over the rest of nature, including over other human beings.

However this destiny of civilization was not inherent as history teaches us. This definition is one particular mode of civilization that became prevalent. During human history there has been a plethora of forms of civilizations. Our role as revolutionaries is to reconstruct the civilizational paradigm.

The democratic nation is synonymous with society, and produces all value including that which the state extracts. Creative enterprise and wealth production originates in society from small scale business, artisans and inventors, and anybody driven by intent or ambition to create works.

Within society, there are multiple coexisting nations which are communities of people sharing language, history, ethnicity or culture. For example there could be a nation based on spiritual belief, a nation of women, or a distinct cultural nation.

The nation state is an extreme variant of the state civilization tendency. Like early state civilizations, the development of the French nation-state was more effective at seizing the wealth of society to mobilize in war against the existing empires of the time.

Soon after, the remaining systems were forced to adopt the nation state system, including its ideology of nationalism. It is no mistake that the nation state tends towards nationalism and fascism including the worst genocides in human history. Nationalism is a blind religion supplanting religious ideologies weakened by secularism. However nationalism is separate from patriotism.

Loving one's country for which you have struggled and fought over for centuries or even millenia as an ethnic community or nation, which you have made your homeland in this long struggle, represents a sacred value.

~ Ocalan's "PKK and Kurdish Question in the 21st century"

Defining the State

The state is a centralized organization that imposes and enforces rules over a population through the monopoly on the legitimate use of violence. In discussing the rise of militarism, Ocalan says:

Essentially, he attempted to establish his authority over two key groups: the hunters at his side and the women he was trying to confine to the home. Along the way, as shamans (proto-priests) and gerontocratic elements (groups of elders) joined the crafty strongman, the first hierarchical authority was formed in many societies in various forms.

Section called "Society’s Militarism Problem" from "The Sociology of Freedom"

The state is defined as:

1. Ideological hegemony represented by a system of priests and shamans in pre-state formations. Today this is the media industry, schools, and big tech (for example "fake news" and surveillance systems).
2. Monopolization on the use of violence through military and police. Powerful commanders like Gilgamesh conquered neighbouring tribes, creating nascent state polities whose main business model was to hunt and enslave barbarian tribes. This enabled state to expand agricultural output which they seized through taxation.
3. State bureaucracy and administration represented in tribal societies and proto-states through a council of elders. This arm of the state also includes scientific research institutes, state psychology groups and various forms of manipulation including modern AI and data harvesting. This tendency is a misappropriation of scientific methods to serve power, thus retarding scientific and technological development and impoverishing society by depriving it of its great benefits.

The state is a parasite on society, extracting value created. There are many historical stateless societies such as the Medean Confederation, the Iroquiois Confederation, the ninja republics of Iga and Kōga, the Swiss pre-Sonderbund Confederation Helvetica, and Cossack society.

Government is a system or people administrating a society. Although most governments are nation-states, we can create stateless societies with autonomous governments. Within a free society government is local, broadly democratic, and autonomous. Society is widely engaged at every level in decision making through local people's councils, as well as possessing the use of violence through a system of gun ownership and local militias. Government also answers to a network of various interest groups from various nations such as women or youth.

Modernity and the Subject of Ideology

Modernity was born in the "age of reason" and represents the overturning of prevailing religious ideas and rejection of tradition in favour of secularization. Modernity has a mixed legacy which includes alienation, commodity fetishism, scientific positivism, and rationalism.

During this period of modernity 4 major ideologies developed, each with their own specific subject as its focus.

• Liberalism and its subject of the individual. Individuals are atomic units existing under the state system which guarantees them certain bargains in the form of laws and rights.
• Communism which focused on the concept of class warfare and economic justice through state power.
• Fascism which put the volk or state at the center of society, whereby all resources would be mobilized to serve the state.
• Anarchism with its critiques of power and favouring social freedom.

The particular form of modernity that is predominant can be characterized as capitalist modernity. Capitalism, otherwise referred to by others as corporatism can be likened to a religion, whereby a particular elite class having no ideology except self profit uses the means of the state to protect its own interests and extract the wealth of society through nefarious means. In some ways, it is a parasite on the state.

Agorist free markets is the democratic tendency of economy. The word 'economy' derives from the Ancient Greek 'oikonomos' which means household management. Economy was, during ancient periods, connected with nature, the role of motherhood, life, and freedom. It was believed that wealth was derived from the quality of our lived environments. The Kurds use the feminine word 'mal' to refer to the house, while the masculine variant refers to actual property. Later during the Roman period, economy came to be understood as the accumulation of property in the form of number of slaves owned, amount of land seized, or the quantity of money.

The subject of our ideology is the moral and political society. Society exists within a framework of morality and politics. Here we use politics to refer not to red team vs blue team, but instead all social activity concerned with our security, necessity, and life. A society can only be free when it has its own morality and politics. The state seeks to keep society weak by depriving it of morality and replacing society's politics with statecraft.

The Extinction of Humanity

During the 20th century, liberals, communists, and fascists vyed for state power each promising a new form of society. State power existed with these external ideological justifications.

With the end of the Soviet Union, and the end of history (according to liberalism), state power morphed into pure domination and profit. The system simply became a managerial form of raw power over society without purpose or aim. Wars such as the Iraq War were invented by neoliberals to breathe a new purpose into society. Indeed, there is no more effective means to support despotism than war.

Today the military industrial complex has grown into a gigantic leviathan that threatens the world driving economies into an ever greater spiral of desperation. The push for the development of automated weapons, aerial drones, and ninja missiles that eliminate all space for human resistance against tyranny.

Meanwhile social credit scoring is being introduced as CBDCs with incentivization schemes such as UBI. Such systems will give more effective means for the seizure of wealth by the state from society, centralizing economic power within an already deeply corrupt elite class.

Liberal ideologies have made people indifferent to their own situation, turning society inward and focused on social media, unable to organize together to oppose rising authoritarianism. Liberalism is essentially a tendency towards extinction or death.

Nature, Life, Freedom

Nature is the center of spiritual belief. Humanity is an aspect of nature. Nature is more than the number of trees. It is the going up, the ascending of life. Through struggle, we overcome obstacles, becoming harder and stronger along the way. This growth makes us more human and closer with nature.

People naturally feel an empathy with nature such as when an animal is injured or generous feelings towards the young of any species. This feeling was put in us by evolution. We feel an attachment and empathy towards our lived environment and want to see it improve. This feeling is mother nature speaking through us. The more in touch we are with this deeper feeling, the more free we are since we are able to develop as higher human beings.

Freedom does not mean the ability to be without constraint or enact any wild fantasy at a moment's notice. Freedom means direct conscious action with power that drives us to ascend. Nature is full of interwoven threads of organisms vying for influence or power, with time doing an ordered dance punctuated by inflection points of change. It is during these moments that our ability of foresight and prescience allows us to deeply affect events along alternative trajectories.

Re-Evaluating Anarchism

Anarchists had the correct critique & analysis of power. In particular seeing that the nation state would grow into a monster that would consume society. However they were the least equipped of all the other ideologies during modernity to enact their vision and put their ideas into practice.

• They fell victim to the same positivist forces that they claimed to be fighting against.
• They lacked a coherent vision and had little strategy or roadmap for how the revolution would happen.
• Their utopian demand that the state must be eliminated immediately and at all costs meant they were not able to plan how that would happen.
• Their opposition to all forms of authority, even legitimate leadership, meant they were ineffective at organizing revolutionary forces.

Revolutionary Objectives

• Our movement is primarily a spiritual one. One cannot understand Christianity by studying its system of churches, since primarily it is a body of teachings. Likewise, the core of our movement is in our philosophy, ideas, and concepts, which then inform our ideas on governance and economics.
• We must build a strong intellectual fabric that inoculates us and fosters resilience, as well as equipping us with the means to be effective in our work.
• There are two legacies in technology, one informed by state civilization and the other by society. The technology we create is to solve problems that society and aligned communities have.

Definition of Democratic Civilization

From 'The Sociology of Freedom: Manifesto of the Democratic Civilization, Volume 3' by Abdullah Ocalan.

Annotations are our own. The text is otherwise unchanged.

What is the subject of moral and political society?

The school of social science that postulates the examination of the existence and development of social nature on the basis of moral and political society could be defined as the democratic civilization system. The various schools of social science base their analyses on different units. Theology and religion prioritize society. For scientific socialism, it is class. The fundamental unit for liberalism is the individual. There are, of course, schools that prioritize power and the state and others that focus on civilization. All these unit-based approaches must be criticized, because, as I have frequently pointed out, they are not historical, and they fail to address the totality. A meaningful examination would have to focus on what is crucial from the point of view of society, both in terms of history and actuality. Otherwise, the result will only be one more discourse.

Identifying our fundamental unit as moral and political society is significant, because it also covers the dimensions of historicity and totality. Moral and political society is the most historical and holistic expression of society. Morals and politics themselves can be understood as history. A society that has a moral and political dimension is a society that is the closest to the totality of all its existence and development. A society can exist without the state, class, exploitation, the city, power, or the nation, but a society devoid of morals and politics is unthinkable. Societies may exist as colonies of other powers, particularly capital and state monopolies, and as sources of raw materials. In those cases, however, we are talking about the legacy of a society that has ceased to be.

Individualism is a state of war

There is nothing gained by labeling moral and political society—the natural state of society—as slave-owning, feudal, capitalist, or socialist. Using such labels to describe society masks reality and reduces society to its components (class, economy, and monopoly). The bottleneck encountered in discourses based on such concepts as regards the theory and practice of social development stems from errors and inadequacies inherent in them. If all of the analyses of society referred to with these labels that are closer to historical materialism have fallen into this situation, it is clear that discourses with much weaker scientific bases will be in a much worse situation. Religious discourses, meanwhile, focus heavily on the importance of morals but have long since turned politics over to the state. Bourgeois liberal approaches not only obscure the society with moral and political dimensions, but when the opportunity presents itself they do not hesitate to wage war on this society. Individualism is a state of war against society to the same degree as power and the state is. Liberalism essentially prepares society, which is weakened by being deprived of its morals and politics, for all kinds of attacks by individualism. Liberalism is the ideology and practice that is most anti-society.

The rise of scientific positivism

In Western sociology (there is still no science called Eastern sociology) concepts such as society and civilization system are quite problematic. We should not forget that the need for sociology stemmed from the need to find solutions to the huge problems of crises, contradictions, and conflicts and war caused by capital and power monopolies. Every branch of sociology developed its own thesis about how to maintain order and make life more livable. Despite all the sectarian, theological, and reformist interpretations of the teachings of Christianity, as social problems deepened, interpretations based on a scientific (positivist) point of view came to the fore. The philosophical revolution and the Enlightenment (seventeenth and eighteenth centuries) were essentially the result of this need. When the French Revolution complicated society’s problems rather than solving them, there was a marked increase in the tendency to develop sociology as an independent science. Utopian socialists (Henri de Saint-Simon, Charles Fourier, and Pierre-Joseph Proudhon), together with Auguste Comte and Émile Durkheim, represent the preliminary steps in this direction. All of them are children of the Enlightenment, with unlimited faith in science. They believed they could use science to re-create society as they wished. They were playing God. In Hegel’s words, God had descended to earth and, what’s more, in the form of the nation-state. What needed to be done was to plan and develop specific and sophisticated “social engineering” projects. There was no project or plan that could not be achieved by the nation-state if it so desired, as long as it embraced the “scientific positivism” and was accepted by the nation-state!

Capitalism as an iron cage

British social scientists (political economists) added economic solutions to French sociology, while German ideologists contributed philosophically. Adam Smith and Hegel in particular made major contributions. There was a wide variety of prescriptions from both the left and right to address the problems arising from the horrendous abuse of the society by the nineteenth-century industrial capitalism. Liberalism, the central ideology of the capitalist monopoly has a totally eclectic approach, taking advantage of any and all ideas, and is the most practical when it comes to creating almost patchwork-like systems. It was as if the right- and left- wing schematic sociologies were unaware of social nature, history, and the present while developing their projects in relation to the past (the quest for the “golden age” by the right) or the future (utopian society). Their systems would continually fragment when they encountered history or current life. The reality that had imprisoned them all was the “iron cage” that capitalist modernity had slowly cast and sealed them in, intellectually and in their practical way of life. However, Friedrich Nietzsche’s ideas of metaphysicians of positivism or castrated dwarfs of capitalist modernity bring us a lot closer to the social truth. Nietzsche leads the pack of rare philosophers who first drew attention to the risk of society being swallowed up by capitalist modernity. Although he is accused of serving fascism with his thoughts, his foretelling of the onset of fascism and world wars was quite enticing.

The increase in major crises and world wars, along with the division of the liberal center into right- and left-wing branches, was enough to bankrupt positivist sociology. In spite of its widespread criticism of metaphysics, social engineering has revealed its true identity with authoritarian and totalitarian fascism as metaphysics at its shallowest. The Frankfurt School is the official testimonial of this bankruptcy. The École Annales and the 1968 youth uprising led to various postmodernist sociological approaches, in particular Immanuel Wallerstein’s capitalist world-system analysis. Tendencies like ecology, feminism, relativism, the New Left, and world-system analysis launched a period during which the social sciences splintered. Obviously, financial capital gaining hegemony as the 1970s faded also played an important role. The upside of these developments was the collapse of the hegemony of Eurocentric thought. The downside, however, was the drawbacks of a highly fragmented social sciences.

The problems of Eurocentric sociology

Let’s summarize the criticism of Eurocentric sociology:

1. Positivism, which criticized and denounced both religion and metaphysics, has not escaped being a kind of religion and metaphysics in its own right. This should not come as a surprise. Human culture requires metaphysics. The issue is to distinguish good from bad metaphysics.

2. An understanding of society based on dichotomies like primitive vs. modern, capitalist vs. socialist, industrial vs. agrarian, progressive vs. reactionary, divided by class vs. classless, or with a state vs. stateless prevents the development of a definition that comes closer to the truth of social nature. Dichotomies of this sort distance us from social truth.

3. To re-create society is to play the modern god. More precisely, each time society is recreated there is a tendency to form a new capital and power-state monopoly. Much like medieval theism was ideologically connected to absolute monarchies (sultanates and shāhanshāhs), modern social engineering as recreation is essentially the divine disposition and ideology of the nation-state. Positivism in this regard is modern theism.

4. Revolutions cannot be interpreted as the re-creation acts of society. When thusly understood they cannot escape positivist theism. Revolutions can only be defined as social revolutions to the extent that they free society from excessive burden of capital and power.

5. The task of revolutionaries cannot be defined as creating any social model of their making but more correctly as playing a role in contributing to the development of moral and political society.

6. Methods and paradigms to be applied to social nature should not be identical to those that relate to first nature. While the universalist approach to first nature provides results that come closer to the truth (I don’t believe there is an absolute truth), relativism in relation to social nature may get us closer to the truth. The universe can neither be explained by an infinite universalist linear discourse or by a concept of infinite similar circular cycles.

7. A social regime of truth needs to be reorganized on the basis of these and many other criticisms. Obviously, I am not talking about a new divine creation, but I do believe that the greatest feature of the human mind is the power to search for and build truth.

A new social science

In light of these criticisms, I offer the following suggestions in relation to the social science system that I want to define:

A more humane social nature

1. I would not present social nature as a rigid universalist truth with mythological, religious, metaphysical, and scientific (positivist) patterns. Understanding it to be the most flexible form of basic universal entities that encompass a wealth of diversities but are tied down to conditions of historical time and location more closely approaches the truth. Any analysis, social science, or attempt to make practical change without adequate knowledge of the qualities of social nature may well backfire. The monotheistic religions and positivism, which have appeared throughout the history of civilization claiming to have found the solution, were unable to prevent capital and power monopolies from gaining control. It is therefore their irrevocable task, if they are to contribute to moral and political society, to develop a more humane analysis based on a profound self-criticism.

2. Moral and political society is the main element that gives social nature its historical and complete meaning and represents the unity in diversity that is basic to its existence. It is the definition of moral and political society that gives social nature its character, maintains its unity in diversity, and plays a decisive role in expressing its main totality and historicity. The descriptors commonly used to define society, such as primitive, modern, slave-owning, feudal, capitalist, socialist, industrial, agricultural, commercial, monetary, statist, national, hegemonic, and so on, do not reflect the decisive features of social nature. On the contrary, they conceal and fragment its meaning. This, in turn, provides a base for faulty theoretical and practical approaches and actions related to society.

Protecting the social fabric

3. Statements about renewing and re-creating society are part of operations meant to constitute new capital and power monopolies in terms of their ideological content. The history of civilization, the history of such renewals, is the history of the cumulative accumulation of capital and power. Instead of divine creativity, the basic action the society needs most is to struggle against factors that prevent the development and functioning of moral and political social fabric. A society that operates its moral and political dimensions freely, is a society that will continue its development in the best way.

4. Revolutions are forms of social action resorted to when society is sternly prevented from freely exercising and maintaining its moral and political function. Revolutions can and should be accepted as legitimate by society only when they do not seek to create new societies, nations, or states but to restore moral and political society its ability to function freely.

5. Revolutionary heroism must find meaning through its contributions to moral and political society. Any action that does not have this meaning, regardless of its intent and duration, cannot be defined as revolutionary social heroism. What determines the role of individuals in society in a positive sense is their contribution to the development of moral and political society.

6. No social science that hopes to develop these key features through profound research and examination should be based on a universalist linear progressive approach or on a singular infinite cyclical relativity. In the final instance, instead of these dogmatic approaches that serve to legitimize the cumulative accumulation of capital and power throughout the history of civilization, social sciences based on a non-destructive dialectic methodology that harmonizes analytical and emotional intelligence and overcomes the strict subject-object mold should be developed.

The framework of moral and political society

The paradigmatic and empirical framework of moral and political society, the main unit of the democratic civilization system, can be presented through such hypotheses. Let me present its main aspects:

1. Moral and political society is the fundamental aspect of human society that must be continuously sought. Society is essentially moral and political.

2. Moral and political society is located at the opposite end of the spectrum from the civilization systems that emerged from the triad of city, class, and state (which had previously been hierarchical structures).

3. Moral and political society, as the history of social nature, develops in harmony with the democratic civilization system.

4. Moral and political society is the freest society. A functioning moral and political fabric and organs is the most decisive dynamic not only for freeing society but to keep it free. No revolution or its heroines and heroes can free the society to the degree that the development of a healthy moral and political dimension will. Moreover, revolution and its heroines and heroes can only play a decisive role to the degree that they contribute to moral and political society.

5. A moral and political society is a democratic society. Democracy is only meaningful on the basis of the existence of a moral and political society that is open and free. A democratic society where individuals and groups become subjects is the form of governance that best develops moral and political society. More precisely, we call a functioning political society a democracy. Politics and democracy are truly identical concepts. If freedom is the space within which politics expresses itself, then democracy is the way in which politics is exercised in this space. The triad of freedom, politics, and democracy cannot lack a moral basis. We could refer to morality as the institutionalized and traditional state of freedom, politics, and democracy.

6. Moral and political societies are in a dialectical contradiction with the state, which is the official expression of all forms of capital, property, and power. The state constantly tries to substitute law for morality and bureaucracy for politics. The official state civilization develops on one side of this historically ongoing contradiction, with the unofficial democratic civilization system developing on the other side. Two distinct typologies of meaning emerge. Contradictions may either grow more violent and lead to war or there may be reconciliation, leading to peace.

7. Peace is only possible if moral and political society forces and the state monopoly forces have the will to live side by side unarmed and with no killing. There have been instances when rather than society destroying the state or the state destroying society, a conditional peace called democratic reconciliation has been reached. History doesn’t take place either in the form of democratic civilization—as the expression of moral and political society—or totally in the form of civilization systems—as the expression of class and state society. History has unfolded as intense relationship rife with contradiction between the two, with successive periods of war and peace. It is quite utopian to think that this situation, with at least a five-thousand-year history, can be immediately resolved by emergency revolutions. At the same time, to embrace it as if it is fate and cannot be interfered with would also not be the correct moral and political approach. Knowing that struggles between systems will be protracted, it makes more sense and will prove more effective to adopt strategic and tactical approaches that expand the freedom and democracy sphere of moral and political society.

8. Defining moral and political society in terms of communal, slave-owning, feudal, capitalist, and socialist attributes serves to obscure rather than elucidate matters. Clearly, in a moral and political society there is no room for slave-owning, feudal, or capitalist forces, but, in the context of a principled reconciliation, it is possible to take an aloof approach to these forces, within limits and in a controlled manner. What’s important is that moral and political society should neither destroy them nor be swallowed up by them; the superiority of moral and political society should make it possible to continuously limit the reach and power of the central civilization system. Communal and socialist systems can identify with moral and political society insofar as they themselves are democratic. This identification is, however, not possible, if they have a state.

9. Moral and political society cannot seek to become a nation-state, establish an official religion, or construct a non-democratic regime. The right to determine the objectives and nature of society lies with the free will of all members of a moral and political society. Just as with current debates and decisions, strategic decisions are the purview of society’s moral and political will and expression. The essential thing is to have discussions and to become a decision-making power. A society who holds this power can determine its preferences in the soundest possible way. No individual or force has the authority to decide on behalf of moral and political society, and social engineering has no place in these societies.

Liberating democratic civilization from the State

When viewed in the light of the various broad definitions I have presented, it is obvious that the democratic civilization system—essentially the moral and political totality of social nature—has always existed and sustained itself as the flip side of the official history of civilization. Despite all the oppression and exploitation at the hands of the official world-system, the other face of society could not be destroyed. In fact, it is impossible to destroy it. Just as capitalism cannot sustain itself without noncapitalist society, civilization— the official world system— also cannot sustain itself without the democratic civilization system. More concretely the civilization with monopolies cannot sustain itself without the existence of a civilization without monopolies. The opposite is not true. Democratic civilization, representing the historical flow of the system of moral and political society, can sustain itself more comfortably and with fewer obstacles in the absence of the official civilization.

I define democratic civilization as a system of thought, the accumulation of thought, and the totality of moral rules and political organs. I am not only talking about a history of thought or the social reality within a given moral and political development. The discussion does, however, encompass both issues in an intertwined manner. I consider it important and necessary to explain the method in terms of democratic civilization’s history and elements, because this totality of alternate discourse and structures are prevented by the official civilization. I will address these issues in subsequent sections.

Recommended Books

• Core Texts
• Philosophy
• Python
• C
• Rust
• Mathematics
  • Abstract Algebra
  • Elliptic Curves
  • Algebraic Geometry
    • Commutative Algebra
  • Algebraic Number Theory
• Cryptography
  • ZK
• Miscellaneous

Core Texts

• Manifesto for a Democratic Civilization parts 1, 2 & 3 by Ocalan. This are a good high level overview of history, philosophy and spiritualism talking about the 5000 year legacy of state civilization, the development of philosophy and humanity's relationship with nature.
• New Paradigm in Macroeconomics by Werner explains how economics and finance work on a fundamental level. Emphasizes the importance of economic networks in issuing credit, and goes through all the major economic schools of thought.
• Authoritarian vs Democratic Technics by Mumford is a short 10 page summary of his books The Myth of the Machine parts 1 & 2. Mumford was a historian and philosopher of science and technology. His books describe the two dominant legacies within technology; one enslaving humanity, and the other one liberating humanity from the state.
• GNU and Free Software texts

Philosophy

• The Story of Philosophy by Will Durant
• The Sovereign Individual is very popular among crypto people. Makes several prescient predictions including about cryptocurrency, algorithmic money and the response by nation states against this emeregent technology. Good reading to understand the coming conflict between cryptocurrency and states.

Python

• Python Crash Course by Eric Matthes. Good beginner text.
• O'Reilly books: Python Data Science, Python for Data Analysis

C

• The C Programming Language by K&R (2nd Edition ANSI C)

Rust

• The Rust Programming Language from No Starch Press. Good intro to learn Rust.
• Rust for Rustaceans from No Starch Press is an advanced Rust book.

Mathematics

Abstract Algebra

• Pinter is your fundamental algebra text. Everybody should study this book. My full solutions here.
• Basic Abstract Algebra by Dover is also a good reference.
• Algebra by Dummit & Foote. The best reference book you will use many times. Just buy it.
• Algebra by Serge Lang. More advanced algebra book but often contains material not found in the D&F book.

Elliptic Curves

• Washington is a standard text and takes a computational approach. The math is often quite obtuse because he avoids introducing advanced notation, instead keeping things often in algebra equations.
• Silverman is the best text but harder than Washington. The material however is rewarding.

Algebraic Geometry

• Ideals, Varieties and Algorithms by Cox, Little, O'Shea. They have a follow up advanced graduate text called Using Algebraic Geometry. It's the sequel book explaining things that were missing from the first text.
• Hartshorne is a famous text.

Commutative Algebra

• Atiyah-MacDonald. Many independent solution sheets online if you search for them. Or ask me ;)

Algebraic Number Theory

• Algebraic Number Theory by Frazer Jarvis, chapters 1-5 (~100 pages) is your primary text. Book is ideal for self study since it has solutions for exercises.
• Introductory Algebraic Number Theory by Alaca and Williams is a bit dry but a good supplementary reference text.
• Elementary Number Theory by Jones and Jones, is a short text recommended in the preface to the Jarvis book.
• Algebraic Number Theory by Milne, are course notes written which are clear and concise.
• Short Algebraic Number Theory course, see also the lecture notes.
• Cohen book on computational number theory is a gold mine of standard algos.
• LaVeque Fundamentals of Number Theory

Cryptography

ZK

• Proofs, Arguments, and Zero-Knowledge by Justin Thaler.

Miscellaneous

• Cryptoeconomics by Eric Voskuil.

Compiling and Running a Node

Since this is still an early phase, we will not be installing any of the software system-wide. Instead, we'll be running all the commands from the git repository, so we're able to easily pull any necessary updates.

Compiling

Refer to the main README file for instructions on how to install Rust and necessary deps.

Once you have the repository in place, and everything is installed, we can compile the darkfid node and the drk wallet CLI:

$ make darkfid drk

This process will now compile the node and the wallet CLI tool. When finished, we can begin using the network. Run darkfid once so that it spawns its config file on your system. This config file will be used by darkfid in order to configure itself. The defaults are already preset for using the testnet network.

$ ./darkfid
Config file created in "~/.config/darkfi/darkfid_config.toml". Please review it and try again.

Running

Once that's in place, you can run it again and darkfid will start, create the necessary keys for validation of blocks and transactions, and begin syncing the blockchain. Keep it running, and you should see a Blockchain is synced! message after some time.

$ ./darkfid

Now it's time to initialize your wallet. For this we use a separate wallet CLI which is created to interface with the smart contract used for payments and swaps.

We simply have to initialize a wallet, and create a keypair:

$ ./drk wallet --initialize
$ ./drk wallet --keygen

The second command will print out your new DarkFi address where you can receive payments. Take note of it. Alternatively, you can always retrieve it using:

$ ./drk wallet --address

In order to receive incoming coins, you'll need to use the drk tool to subscribe on darkfid so you can receive notifications for incoming blocks. The blocks have to be scanned for transactions, and to find coins that are intended for you. In another terminal, you can run the following commands to first scan the blockchain, and then to subscribe to new blocks:

$ ./drk scan
$ ./drk subscribe

Now you can leave the subscriber running. In case you stop it, just run drk scan again until the chain is fully scanned, and then you should be able to subscribe again.

Local Deployment

For development we recommend running master. First we modify the constants specifically for a local testnet. This step is optional but you might find scanning takes a long time otherwise.

cd contrib/localnet/darkfid-single-node/
./tmux_sessions.sh now
cd ../../../
make darkfid

You can run a single consensus full node using this command:

./tmux_sessions.sh -v

Advanced Usage

To run a node in full debug mode:

LOG_TARGETS="\!sled,\!net" ./darkfid -v | tee /tmp/darkfid.log

The sled and net targets are very noisy and slow down the node so we disable those.

We can now view the log, and grep through it.

tail -n +0 -f /tmp/darkfid.log | grep -a --line-buffered -v DEBUG

Airdrops

Now you have your wallet set up. Let's proceed with getting some tokens from the faucet. The testnet has a running faucet which is able to airdrop native network tokens.

So let's airdrop some of these into our wallet:

$ ./drk airdrop 42.69

There is a limit of 100 for testnet airdrops currently.

Note: you have to wait some minutes between airdrops since they're rate-limited.

On success, you should see a transaction ID. If successful, the airdrop transactions will now be in the consensus' mempool, waiting for inclusion in the next block. Depending on the network, finalization of the blocks could take some time. You'll have to wait for this to happen. If your drk subscribe blocks is running, then after some time your balance should be in your wallet.

You can check your wallet balance using drk:

$ ./drk wallet --balance

Aliases

To make our life easier, we can create token ID aliases, so when we are performing transactions with them, we can use that instead of the full token ID. Multiple aliases per token ID are supported.

Example addition:

$ ./drk alias add {ALIAS} {TOKEN}

So let's add the native token as DARK by executing:

$ ./drk alias add DARK 12ea8e3KVuBhmSnr29iV34Zd2RsD1MEeGk9xJhcipUqx

From now on, we can use DARK to refer to the native token when executing transactions using it.

We can also list all our aliases using:

$ ./drk alias show

Note: these aliases are only local to your machine. When exchanging with other users, always verify that your aliases' token IDs match.

Minting tokens

On the DarkFi network, we're also able to mint custom tokens with some supply. To do this, we need to generate a mint authority keypair, and derive a token ID from it. We can simply do this by executing the following command:

$ ./drk token generate-mint

This will generate a new token mint authority and will tell you what your new token ID is. For this tutorial we will need two tokens so execute the command again to generate another one.

You can list your mint authorities with:

$ ./drk token list

Now let's add those two token IDs to our aliases:

$ ./drk alias add WCKD {TOKEN1}
$ ./drk alias add MLDY {TOKEN2}

Now let's mint some tokens for ourselves. First grab your wallet address, and then create the token mint transaction, and finally - broadcast it:

$ ./drk wallet --address
$ ./drk token mint WCKD 42.69 {YOUR_ADDRESS} > mint_tx
$ ./drk broadcast < mint_tx

$ ./drk token mint MLDY 20.0 {YOUR_ADDRESS} > mint_tx
$ ./drk broadcast < mint_tx

Now the transaction should be published to the network. If you have an active block subscription (which you can do with drk subscribe blocks), then when the transaction is finalized, your wallet should have your new tokens listed when you request to see the balance.

Payments

Using the tokens we minted, we can make payments to other addresses. Let's try to send some WCKD tokens to 8sRwB7AwBTKEkyTW6oMyRoJWZhJwtqGTf7nyHwuJ74pj:

$ ./drk transfer 2.69 WCKD \
    8sRwB7AwBTKEkyTW6oMyRoJWZhJwtqGTf7nyHwuJ74pj > payment_tx

The above command will create a transfer transaction and place it into the file called payment_tx. Then we can broadcast this transaction to the network:

$ ./drk broadcast < payment_tx

On success we'll see a transaction ID. Now again the same finalization process has to occur and 8sRwB7AwBTKEkyTW6oMyRoJWZhJwtqGTf7nyHwuJ74pj will receive the tokens you've sent.

We can see the spent coin in our wallet.

$ ./drk wallet --coins

We have to wait until the next block to see our change balance reappear in our wallet.

$ ./drk wallet --balance

Atomic Swaps

In order to do an atomic swap with someone, you will first have to come to a consensus on what tokens you wish to swap. For example purposes, let's say you want to swap 40 WCKD (which is the balance you should have left over after doing the payment from the previous page) for your counterparty's 20 MLDY. For this tutorial the counterparty is yourself.

To protect your anonymity from the counterparty, the swap can only send entire coins. To create a smaller coin denomination, send yourself the amount you want to swap. Then check you have a spendable coin to swap with:

$ ./drk wallet --coins

You'll have to initiate the swap and build your half of the swap tx:

$ ./drk otc init -v 40.0:20.0 -t WCKD:MLDY > half_swap

Then you can send this half_swap file to your counterparty and they can create the other half by running:

$ ./drk otc join < half_swap > full_swap

They will sign the full_swap file and send it back to you. Finally, to make the swap transaction valid, you need to sign it as well, and broadcast it:

$ ./drk otc sign < full_swap > signed_swap
$ ./drk broadcast < signed_swap

On success, you should see a transaction ID. This transaction will now also be in the mempool, so you should wait again until it's finalized.

After a while you should see the change in balances in your wallet:

$ ./drk wallet --balance

If you see your counterparty's tokens, that means the swap was successful. In case you still see your old tokens, that could mean that the swap transaction has not yet been finalized.

DAO

On the testnet, we are also able to create an anonymous DAO. Using the drk CLI tool, we have a dao subcommand that can perform the necessary operations.

You can find a script in contrib/localnet/darkfid-single-node/run-dao-test.sh which automatically does all the commands in this tutorial. Just be sure to read the comment at the top of the file first.

Let's create a DAO with the following parameters:

• Proposer limit: 20
• Quorum: 10
• Approval ratio: 0.67
• Governance token: MLDY

You can see what these parameters mean with the help command.

$ ./drk help dao create

Let's create our DAO.

$ ./drk dao create 20 10 0.67 MLDY > dao.dat
$ ./drk dao view < dao.dat

The view command will show us the parameters. If everything looks fine, we can now import it into our wallet:

./drk dao import MiladyMakerDAO < dao.dat
./drk dao list
./drk dao list MiladyMakerDAO

Minting

If parameters are shown, this means the DAO was successfully imported into our wallet. The DAO's index in our wallet is 1, so we'll use that to reference it. Now we can create a transaction that will mint the DAO on-chain, and broadcast it:

./drk dao mint MiladyMakerDAO > dao_mint_tx
./drk broadcast < dao_mint_tx

Now the transaction is broadcasted to the network. Wait for it to finalize, and if your drk is subscribed, after finalization you should see a leaf_position and a transaction ID when running dao list MiladyMakerDAO.

Sending money to the treasury

Let's send some tokens to the DAO's treasury so we're able to make a proposal to send those somewhere. First find the DAO bulla and the DAO public key with dao list and then create a transfer transaction:

$ ./drk dao list MiladyMakerDAO
$ ./drk transfer 10 WCKD {DAO_PUBLIC_KEY} \
    --dao {DAO_BULLA} > dao_transfer
$ ./drk broadcast < dao_transfer

Wait for it to finalize, and if subscribed, you should see the DAO receive the funds:

$ ./drk dao balance MiladyMakerDAO

Creating a proposal

Now that the DAO has something in its treasury, we can create a proposal to send it somewhere. Let's send 5 of the 10 tokens to our address (we can find that with drk wallet --address):

$ ./drk dao propose MiladyMakerDAO {YOUR_ADDRESS} 5 WCKD > proposal_tx
$ ./drk broadcast < proposal_tx

Once finalized and scanned, the proposal should be viewable in the wallet. We can see this with the proposal subcommands:

$ ./drk dao proposals MiladyMakerDAO
$ ./drk dao proposal MiladyMakerDAO 1

Voting on a proposal

Now the DAO members are ready to cast their votes. First lets check the dao vote subcommand usage.

$ drk help dao vote
Vote on a given proposal

Usage: drk dao vote <DAO_ALIAS> <PROPOSAL_ID> <VOTE> <VOTE_WEIGHT>

Arguments:
  <DAO_ALIAS>    Name or numeric identifier for the DAO
  <PROPOSAL_ID>  Numeric identifier for the proposal
  <VOTE>         Vote (0 for NO, 1 for YES)
  <VOTE_WEIGHT>  Vote weight (amount of governance tokens)

Lets use our 20 MLDY to vote yes to proposal 1.

$ drk dao vote MiladyMakerDAO 1 1 20 > /tmp/dao-vote.tx
$ drk broadcast < /tmp/dao-vote.tx

Executing the proposal

Once enough votes have been cast that meet the required minimum (quorum) and assuming the yes:no votes ratio is bigger than the approval ratio, then we are ready to finalize the vote. Any DAO member can perform this action.

$ drk dao exec MiladyMakerDAO 1 > /tmp/dao-exec.tx
$ drk broadcast < /tmp/dao-exec.tx

ircd: Strong Anonymity P2P Chat

In DarkFi, we organize our communication using resilient and censorship-resistant infrastructure. For chatting, ircd is a peer-to-peer implementation of an IRC server in which any user can participate anonymously using any IRC frontend and by running the IRC daemon. ircd uses the DarkFi P2P engine to synchronize chats between hosts.

Benefits

• Encrypted using same algorithms as Signal.
• There are no identities. You cannot see who is in the chat.
• Completely anonymous. You can rename yourself easily by using the command /nick foo. This means all messages are unlinkable.
• God-fearing based CLI without soy gui shit.
• p2p decentralized.
• Optionally run it over Tor or Nym for network level anonymity.

Therefore this is the world's most strongly anonymous chat in existence. Nothing else exists like it.

Installation

Follow the instructions in the README to ensure you have all the necessary dependencies.

% git clone https://github.com/darkrenaissance/darkfi.git
% cd darkfi && git checkout v0.4.1
% make ircd

Installation (Android)

This is for Android 64 bit (which is most phones).

1. Setup Docker on your machine which may look like:
   1. Install docker and docker-buildx packages.
   2. Enable the docker daemon service.
   3. Add your user to the docker group and refresh the session (either with su -c $USER or logout/login).
2. Run cd bin/darkirc/ && make docker-android. The resulting file will be called darkirc.aarch64-android. Copy this to your phone.
3. Install Termux and RevolutionIRC on F-Droid.
4. You can access the phone storage from /sdcard/ and copy the file into the Termux home.
5. Run termux-wake-lock. This stops Android suspending the daemon.
6. Run the daemon. You can open new Termux sessions by swiping from the left to bring up the sidebar.
7. Connect the RevolutionIRC frontend.

Logs

The public channels have logs available, and additionally there is a mirror on telegram @darkfi_darkirc channel. You can also message @darkirc_bot with "sub" to avoid doxxing your username. Use "unsub" to unsubscribe.

Usage (DarkFi Network)

Upon compiling ircd as described above, the preconfigured defaults will allow you to connect to the network and start chatting with the rest of the DarkFi community.

First, try to start ircd from your command-line so it can spawn its configuration file in place. The preconfigured defaults will autojoin you to several default channels one of which is #dev where we have weekly meetings, and where the community is most active and talks about DarkFi development.

% ./ircd

ircd will create a configuration file ircd_config.toml by default in ~/.config/darkfi/ you can review and potentially edit. It might be useful if you want to add other channels you want to autojoin (like #philosophy and #memes), or if you want to set a shared secret for some channel in order for it to be encrypted between its participants.

When done, you can run ircd for the second time in order for it to connect to the network and start participating in the P2P protocol:

% ./ircd

Clients

Weechat

In this section, we'll briefly cover how to use the Weechat IRC client to connect and chat with ircd.

Normally, you should be able to install weechat using your distribution's package manager. If not, have a look at the weechat git repository for instructions on how to install it on your computer.

Once installed, we can configure a new server which will represent our ircd instance. First, start weechat, and in its window - run the following commands (there is an assumption that irc_listen in the ircd config file is set to 127.0.0.1:6667):

/server add darkfi localhost/6667 -notls -autoconnect
/save
/quit

This will set up the server, save the settings, and exit weechat. You are now ready to begin using the chat. Simply start weechat and everything should work.

When you join, you will not see any users displayed. This is normal since there is no concept of nicknames or registration on this p2p anonymous chat.

You can change your nickname using /nick foo, and navigate channels using F5/F6 or ALT+X where X is the channel number displayed.

Channels can be moved around using /buffer move N where N is the new position of the buffer in the list. Use /layout store to save the current layout of the buffers.

Network-level privacy

Nodes have knowledge of their peers, including the IP addresses of connected hosts.

DarkFi supports the use of pluggable transports, including Tor and Nym, to provide network-level privacy. As long as there are live seed nodes configured to support a Tor or Nym connection, users can connect to ircd and benefit from the protections offered by these protocols.

Other approaches include connecting via a cloud server or VPN. Research the risks involved in these methods before connecting.

Running a Fullnode

See the script script/run_node.sh for an example of how to deploy a full node which does seed session synchronization, and accepts both inbound and outbound connections.

Global Buffer

Copy this script to ~/.weechat/python/autoload/, and you will create a single buffer which aggregates messages from all channels. It's useful to monitor activity from all channels without needing to look at each one individually.

Emojis

Install the noto fonts to have the full unicode set. Popular Linux distros should have packages for them.

Once installed you can view all the emojis in your terminal. Note, you may need to regenerate your font cache (or just restart) after installing them.

Configuring a Private chat between users

Any two users on the ircd server can establish a fully encrypted communication medium between each other using a basic keypair setup.

Configuring ircd_config.toml

ircd_config.toml should be created by default in ~/.config/darkfi/ when you first run ircd.

Generate a keypair using the following command:

% ircd --gen-keypair

This will generate a Public Key and a Private Key.

Save the Private key safely & add it to the ircd_config.toml file as shown below.

[private_key.”your_private_key_goes_here”]

To share your Public Key with a user over ircd you can use one of the public channels or via an external app like Signal, as plaintext DMs are disabled in ircd.

Note: If you use the ircd's public channel, your message will be publically visible on the IRC chat.

See the example ircd_config.toml for more details

Example

Lets start by configuring our contacts list in the generated ircd_config.toml file (you can also refer to the examples written in the comments of the toml file), let's assume alice and bob want to privately chat after they have each other's public keys:

Alice would add bob to her contact list in her own config file:

[contact.”bob”]
contact_pubkey = “D6UzKA6qCG5Mep16i6pJYkUCQcnp46E1jPBsUhyJiXhb”

And Bob would do the same:

[contact.”alice”]
contact_pubkey = “9sfMEVLphJ4dTX3SEvm6NBhTbWDqfsxu7R2bo88CtV8g”

Lets see an Example where 'alice' sends “Hi” message to 'bob' using the /msg command

 /msg bob Hi

Note for Weechat Client Users:
When you private message someone as shown above, the buffer will not pop in weechat client until you receive a reply from that person.

For example here 'alice' will not see any new buffer on her irc interface for the recent message which she just send to 'bob' until 'bob' replies, but 'bob' will get a buffer shown on his irc client with the message 'Hi'.

Reply from 'bob' to 'alice'

/msg alice welcome!

Or instead of /msg command, you can use:

/query bob hello

This works exactly the same as /msg except it will open a new buffer with Bob in your client regardless.

Note: The contact name is not the irc nickname, it can be anything you want, and you should use it when DMing.

Note: It's always a good idea to save your keys somewhere safe, but in case you lost your Public Key and you still have your Private key in ircd_config.toml file, you recover the Public Key like so:

% ircd --recover-pubkey {your_private_key}

Ircd Local Deployment

These steps below are only for developers who wish to make a testing deployment. The previous sections are sufficient to join the chat.

Seed Node

First you must run a seed node. The seed node is a static host which nodes can connect to when they first connect to the network. The seed_session simply connects to a seed node and runs protocol_seed, which requests a list of addresses from the seed node and disconnects straight after receiving them.

The first time you run the program, a config file will be created in ~/.config/darkfi if you are using Linux or in ~/Library/Application Support/darkfi/ on MacOS. You must specify an inbound accept address in your config file to configure a seed node:

## P2P accept addresses
inbound=["127.0.0.1:11001"]

Note that the above config doesn't specify an external address since the seed node shouldn't be advertised in the list of connectable nodes. The seed node does not participate as a normal node in the p2p network. It simply allows new nodes to discover other nodes in the network during the bootstrapping phase.

Inbound Node

This is a node accepting inbound connections on the network but which is not making any outbound connections.

The external addresses are important and must be correct.

To run an inbound node, your config file must contain the following info:

## P2P accept addresses
inbound=["127.0.0.1:11002"]

## P2P external addresses
external_addr=["127.0.0.1:11002"]

## Seed nodes to connect to 
seeds=["127.0.0.1:11001"]

Outbound Node

This is a node which has 8 outbound connection slots and no inbound connections. This means the node has 8 slots which will actively search for unique nodes to connect to in the p2p network.

In your config file:

## Connection slots
outbound_connections=8

## Seed nodes to connect to 
seeds=["127.0.0.1:11001"]

Attaching the IRC Frontend

Assuming you have run the above 3 commands to create a small model testnet, and both inbound and outbound nodes above are connected, you can test them out using weechat.

To create separate weechat instances, use the --dir command:

weechat --dir /tmp/a/
weechat --dir /tmp/b/

Then in both clients, you must set the option to connect to temporary servers:

/set irc.look.temporary_servers on

Finally you can attach to the local ircd instances:

/connect localhost/6667
/connect localhost/6668

And send messages to yourself.

Notes for developers

Making life easy for others

Write useful commit messages.

If your commit is changing a specific module in the code and not touching other parts of the codebase (as should be the case 99% of the time), consider writing a useful commit message that also mentions which module was changed.

For example, a message like:

added foo

is not as clear as

crypto/keypair: Added foo method for Bar struct.

Also keep in mind that commit messages can be longer than a single line, so use it to your advantage to explain your commit and intentions.

cargo fmt pre-commit hook

To ensure every contributor uses the same code style, make sure you run make fmt before committing. You can force yourself to do this by creating a git pre-commit hook like the following:

#!/bin/sh
if ! cargo +nightly fmt --all -- --check >/dev/null; then
    echo "There are some code style issues. Run 'make fmt' on repo root to fix it."
    exit 1
fi

exit 0

Inside the darkfi project repo, place this script in .git/hooks/pre-commit and make sure it's executable by running chmod +x .git/hooks/pre-commit.

Testing crate features

Our library heavily depends on cargo features. Currently there are more than 650 possible combinations of features to build the library. To ensure everything can always compile and works, we can use a helper for cargo called cargo hack.

The Makefile provided in the repository is already set up to use it, so it's enough to install cargo hack and run make check.

Etiquette

These are not hard and fast rules, but guidance for team members working together. This allows us to coordinate more effectively.

* once we have proper syncing implemented in ircd, these will become less relevant and not needed.

Another option is to run your ircd inside a persistent tmux session, and never miss messages.

Code coverage

You can run codecov tests of the codebase using cargo-llvm-cov:

$ cargo install cargo-llvm-cov
$ make coverage

You can then find the reports in target/llvm-cov/html/index.html

Static binary builds

Using LXC

Using musl-libc, we should be able to produce statically linked binaries from our codebase. A short setup using a Debian system and lxc can be the following:

Setup the LXC container:

# lxc-create -n xbuild-alpine -t alpine -- --release edge
# lxc-start -n xbuild-alpine
# lxc-attach -n xbuild-alpine

Inside the container, once attached, we have to install the required dependencies. We will have to use rustup to get the latest rust nightly, and we also have to compile sqlcipher on our own.

# apk add rustup git musl-dev make gcc openssl-dev openssl-libs-static tcl-dev zlib-static
# wget -O sqlcipher.tar.gz https://github.com/sqlcipher/sqlcipher/archive/refs/tags/v4.5.5.tar.gz
# tar xf sqlcipher.tar.gz
# cd sqlcipher-4.5.5
# ./configure --prefix=/usr/local --disable-shared --enable-static --enable-cross-thread-connections --enable-releasemode
# make -j$(nproc)
# make install
# cd ~
# rustup-init --default-toolchain nightly -y
# source ~/.cargo/env
# rustup target add wasm32-unknown-unknown --toolchain nightly

And now we should be able to build a statically linked binary:

# git clone https://github.com/darkrenaissance/darkfi -b master --depth 1
# cd darkfi
## Uncomment RUSTFLAGS in the main Makefile
# sed -e 's,^#RUSTFLAGS ,RUSTFLAGS ,' -i Makefile
# make darkirc

Native

In certain cases, it might also be possible to build natively by installing the musl toolchain:

$ rustup target add x86_64-unknown-linux-musl --toolchain nightly
## Uncomment RUSTFLAGS in the main Makefile
$ sed -e 's,^#RUSTFLAGS ,RUSTFLAGS ,' -i Makefile
$ make RUST_TARGET=x86_64-unknown-linux-musl darkirc

Contributing

How to get started

1. Join the dev chat, and attend a dev meeting.
2. See the areas of work below. Good areas to get started are with tooling, Python bindings, p2p apps like the DHT.

Every monday 16:00 CET, there is our main dev meeting on our chat. Feel free to join and discuss with other darkfi devs.

In general, the best way to get started is to explore the codebase thoroughly and identify issues and areas of improvement.

Contribute according to your own interests, skills, and topics in which you would like to become more knowledgable. Take initiative. Other darkfi devs can help you as mentors: see the Methodology section of the Study Guide.

Few people are able be an expert in all domains. Choose a topic and specialize. Example specializations are described here. Don't make the mistake that you must become an expert in all areas before getting started. It's best to just jump in.

Finding specific tasks

Tasks are usually noted in-line using code comments. All of these tasks should be resolved and can be considered a priority.

To find them, run the following command:

$ git grep -E 'TODO|FIXME'

Employment

We are only looking for devs right now. If you're not a dev, see the learn section. We offer mentoring. Anybody can become a dev. It's not that hard, you just need focus and dedication.

To be hired as a dev, you must make commits to the repo, preferably more than minor cosmetic changes. It also is useful to have online repositories containing your work. We don't care about degrees or qualifications - many of the best coders don't have any.

Secondly you need to get on our online chat and make yourself known. We are not spending time on social media or proprietary chats like Telegram because we're very busy.

We value people who have initiative. We value this so highly in fact that even if someone is less skilled but shows the ability to learn, we will welcome them and give them everything they need to prosper. Our philosophy is that of training leaders rather than hiring workers. Our team is self-led. We don't have any managers or busybody people. We discuss the problems amongst ourselves and everybody works autonomously on tasks. We don't keep people around who need a manager looking over their shoulder. The work and tasks should be obvious, but to help you along below you will find lists of tasks to get started on.

Areas of work

There are several areas of work that are either undergoing maintenance or need to be maintained:

• Documentation: general documentation and code docs (cargo doc). This is a very important work for example overview page is out of date.
  • We need a tutorial on writing smart contracts. The tutorial could show how to make an anon ZK credential for a service like a forum.
  • Continuing on, it could show how to use the p2p network or event graph to build an anonymous service like a forum.
• TODO and FIXME are throughout the codebase. Find your favourite one and begin hacking.
  • DarkIRC encrypted DMs to nonexistant users should not be allowed.
  • Currently closing DarkIRC with ctrl-c stalls in p2p.stop(). This should be fixed.
  • Add log = path and log_level = debug config setting to DarkIRC
  • StoppableTask should panic when we call stop() on a task that has not been started.
• Tooling: Creating new tools or improving existing ones.
  • Improve the ZK tooling. For example tools to work with txs, smart contracts and ZK proofs.
  • Also document zkrunner and other tools.
• Tests: Throughout the project there are either broken or commented out unit tests, they need to be fixed.
• Cleanup: General code cleanup. for example flattening headers and improving things like in this commit.
• Python bindings: Help ensure wider coverage and cleanup the Python bindings in src/sdk/python/.
  • The event graph could have Python bindings but involves some tricky part integrating Python and Rust async.
  • Bindings for txs, calls and so on. Make a tool in Python for working with various contract params.
• Events System: See the event graph system. We need extra review of the code and improvement of the design. This is a good submodule to begin working on.
• DHT: Currently this is broken and needs fixing.
• p2p Network: this is a good place to start reviewing the code and suggesting improvements. For example maintaining network resiliency. You can also look at apps like darkirc, and the event graph subsystem, and see how to make them more reliable. See also the task manager tau.
  • Implement resource manager. See its implementation in libp2p for inspiration.
• Harder crypto tasks:
  • Money viewing keys
• Eth-DarkFi bridge or atomic swaps. Atomic swaps is probably better since it's trustless and p2p.

Mainnet tasks

Tasks are in no particular order. Use common sense.

1. Finish darkfid with PoW and research and implement XMR merge mining
2. Make darkfi-mmproxy stable and implement what is needed for DarkFi x Monero merge mining
3. Finish dnetview
4. Make eventgraph stable and implement proper unit and integration tests

• Unit tests should test pieces of the eventgraph code
• Integration tests should simulate a P2P network and ensure deterministic state after a simulated run
• Update https://darkrenaissance.github.io/darkfi/misc/event_graph/event_graph.html and make it the specification for the eventgraph implementation.

5. Rework drk (the wallet CLI) to work standalone and make it work with the new darkfid
6. Make tau stable
7. Make darkirc stable
8. Make lilith stable, there is currently some bug that causes connection refusals
9. Implement transaction fees logic
10. Implement contracts deployment logic
11. Revisit all the code inside src/runtime/ and make sure it's safe
12. Implement verifiable encryption for DAO payments
13. DAO should be able to perform arbitrary contract calls, it should act as a voted multisig
14. Implement cross-chain atomic swaps (XMR, ETH, anything applicable)
15. Rework the connection algo for p2p to use black list, grey and white list

• https://eprint.iacr.org/2019/411.pdf (Section 2.2)
• See also P2P Network: Common Mitigations

16. Create a P2P stack test harness in order to be able to easily simulate network behaviour

• Possibly we can create a dummy p2p which can simulate network connections and routing traffic. We can use this to model network behaviour.

17. Implement address/secretkey differentiation

• See WIF

18. Fix bugs and issues in the DAO implementation
19. Perform thorough review of all contracts and their functionalities
20. Randomize outputs in Money::*, and potentially elsewhere where applicable

• This is so the change output isn't always in the same predictable place, and makes identifying which output is the change impossible.

21. Document contracts in the manner of https://darkrenaissance.github.io/darkfi/arch/consensus/stake.html
22. Serial used in money coins

• One solution is: don't accept coins with existing serial in drk.
• We should construct a scheme to derive the serial, evaluate how simple changing the crypto is.
• Malicious users could send you a coin which is unspendable. A poorly implemented wallet would accept such a coin, and if spent then you would be unable to spend the other coin sharing the same serial in your wallet.

23. Separate mining logic from darkfid into a new program and communicate over RPC
24. Python utility tool (swiss army knife) for working with txs, contract calls and params.
25. Python event viewer to inspect and debug the event graph.
26. Fix protocol_address for anonymity. There is a loop sending self addr constantly. We should have this mixed with a bunch of random addrs to avoid leaking our own addr.
27. Add support for colorizing zkas code samples in darkfi book (see arch/dao page)
28. Tutorial creating a ZK credentials scheme.
29. resource manager for p2p (DoS protection, disconnect bad nodes)
30. apply DEP 0001
31. fix channel main_receive_loop() to use Weak
32. configurable MAGIC_BYTES for net code
33. configurable fields for version messages
34. make PeerDiscovery in outbound_session.rs a trait object which is configurable in P2p, but by default is set to PeerSeedDiscovery.

Fuzz testing

Fuzz testing is a method to find important bugs in software. It becomes more powerful as more computing power is allocated to it.

You can help to test DarkFi by running our fuzz tests on your machine. No specialized hardware is required.

As fuzz testing benefits from additional CPU power, a good method for running the fuzzer is to let it run overnight or when you are otherwise not using your device.

Set-up

After running the normal commands to set-up DarkFi as described in the README, run the following commands.

# Install cargo fuzz
$ cargo install cargo-fuzz

Run the following from the DarkFi repo folder:

$ cd fuzz/
$ cargo fuzz list

This will list the available fuzzing targets. Choose one and run it with:

Run

# format: cargo fuzz run TARGET
# e.g. if `serial` is your target:
$ cargo fuzz run --all-features -s none --jobs $(nproc) serial 

This process will run infinitely until a crash occurs or until it is cancelled by the user.

If you are able to trigger a crash, get in touch with the DarkFi team via irc.

Further information on fuzzing in DarkFi is available here.

Troubleshooting

The master branch is considered bleeding-edge so stability issues can occur. If you encounter issues, try the steps below. It is a good idea to revisit these steps periodically as things change. For example, even if you have already installed all dependencies, new ones may have been recently added and this could break your development environment.

• Clear out artifacts and get a fresh build environment:

# Get to the latest commit
$ git pull origin master
# Clean build artifacts
$ make distclean

• Remove Cargo.lock. This will cause Rust to re-evaluate dependencies and could help if there is a version mismatch.

• Ensure all dependencies are installed. Check the README.md and/or run:

$ sh contrib/dependency_setup.sh

• Ensure that you are using the nightly toolchain and are building for wasm32-unknown-unknown. Check README.md for instructions.

• When running a cargo command, use the flag --all-features.

Contributing With Tor

... or how to setup Tor git access with darkfi repo.

We assume you have tor installed locally and access to Tor browser. You can check your tor daemon is running by running this command:

curl --socks5-hostname 127.0.0.1:9050 https://myip.wtf/text

Setting Up Codeberg

Follow these steps:

1. Generate a new SSH key using the command: ssh-keygen -o -a 100 -t ed25519 -f ~/.ssh/id_tor -C foo@foo
2. Next use Tor Browser to make a codeberg account, and get this added to the darkfi repo.
3. Add your key .ssh/id_tor.pub to your account on codeberg.
4. Verify your key by signing the message: echo -n 'XXX' | ssh-keygen -Y sign -n gitea -f ~/.ssh/id_tor where XXX is the string given on codeberg.

SSH Config

You will need BSD netcat installed. Optionally you could use GNU netcat, but the flags are different; replace -x with --proxy ... --proxy-type=socks5.

Add a section in ~/.ssh/config like this:

Host codeberg-tor
    # Use this for debugging errors
    #LogLevel VERBOSE
    User git
    HostName codeberg.org
    IdentitiesOnly yes
    IdentityFile ~/.ssh/id_tor
    ProxyCommand nc -x 127.0.0.1:9050 %h %p

Then test it is working with ssh -T git@codeberg-tor -vvv. Be sure to verify the signatures match those on the codeberg website. To see them, copy this link into Tor Browser: https://docs.codeberg.org/security/ssh-fingerprint/

Adding the Git Remote

The last step is routine:

git remote add codeberg git@codeberg-tor:darkrenaissance/darkfi.git
# Optionally delete the github origin:
git remote rm origin

And then finally it should work. Make sure you use git push -u codeb master to update your main source to codeberg over Tor. You don't want to accidentally git push to github and dox yourself.

Agorism Hackers Study Guide

During the 90s, the crypto-anarchists applied the emerging technology of cryptography to create online zones encoded with the seed of resistance. Cryptocurrency descends from that lineage, and lies at the intersection of economics, politics and technology.

The agorists believed in leveraging economic power to create free and democratic parallel societies. We define revolution as a transformation in the moral and political fabric of society. We can leverage crypto technology for moral and poltical society and create encrypted free zones online.

Money takes many forms, whether cash, credit, loans or debt. The properties of money changes depending on its location, while measures like interest rates and inflation obscure local differences.

The real source of power lies in economic networks. Money is a unit of account between economic networks. By understanding economics, we can use technological techniques to greatly influence the material and political worlds and encode them with our values and philosophy.

Methodology

Our critique of the student-teacher relation, where a teacher dictates a course schedule to a student who has to learn the material, is as follows:

1. Students are not self led, and instead become reliant on an instructor, instead of developing independently.
2. Creativity is supressed since students do not explore and engage with knowledge in a dialectic way.

Instead we provide a system of mentorship. Everybody engages in study and research inside the organization. Subjects are not separated from one another and we encourage people to read multiple subjects in a directed way. Our aim is to train leaders and raise people up.

Leaders must possess:

1. Strategic knowledge to be able to make strong macro analysis and direct activity.
2. Strong techncial skills to directly affect change themselves.

We emphasize a combination of both. Ideas should not gather dust in books. We must put our ideas into action through practice. However, blind undirected action is wasted effort. Therefore we seek to foster both theory and practice in participants.

With the mentorship system, participants are self directed but are under the influence of more senior mentors. If they get stuck, they can ask mentors for assistance to get past difficult concepts or discuss ideas to gain a better understanding. Learning through dialogue is encouraged since it creates stronger bonds and relations between people in the community.

Progression

Mandatory Initial Stage

Everybody in the organization must study philosophy and programming as essential skills. To start there are two objects of study:

1. "Manifesto for a Democratic Civilization" by Ocalan, is 3 separate books. You should complete at least 1 book for the initial stage, and then study the other two as you continue further into later stages.
2. "Project Based Python Programming" this will teach you Python programming which will be an essential skill for any branch you decide to continue onto.

Programming takes time and dedication to become proficient at. Many people give up during the initial phase which can take more than a year. You have to push through it. Once you master programming, it becomes enjoyable and fun. Code is the medium of our organization. We are hacker-artists.

Branches

All branches take roughly the same time to become highly proficient in: around 1-2 years. Even after 6 months, participants can begin using their acquired knowledge in a practical way with small limited tasks. We actively encourage the combination of theory and practice to strengthen one another.

Token Scientist

Token engineering is a new emerging science. Tokens are a breakthrough in building online networks, since we have a means to engineer incentive mechanisms and encourage certain user behaviours.

DeFi protocols in crypto make extensive use of token engineering to design how liquidity flows in and out of networks, and is an important key part of leveraging cryptoeconomic power.

To become proficient in this area requires study of economics, mathematics, and finance. It also makes heavy use of Python programming to build simulations and economic models.

1. "New Paradigm for Macroeconomics" by Werner. This book will take several months to study but is a strong basis for understanding economics.
   1. Notes from the introduction to Werner's book.
   2. Notes on 'Shifting from Central Planning to a Decentralized Economy
2. "Understanding Pure Mathematics". We have a full high school mathematics course. This can also be skipped if you already know maths well.
   1. Continuing on with mathematics, you can learn more about stochastics, statistics, probability and analysis.
3. The DeFi and Token Engineering book.

Software Developer

Software developers create the end result software that others use. They take research and create a product from that research by applying the ideas. Developers can further be focused more on creating prototypes from research, or developing prototypes into polished final products.

To become a senior developer means learning about how the computer works on a deep level, and learning advanced programming skills. It takes time to fully master with a lot of early frustration but is eventually highly rewarding and creative. Developers are highly sought after and rare.

1. Learn from various materials about computer architecture, operating systems, and software architecture.
   1. Books such as the history of UNIX or the mythical man month.
   2. Articles by hintjens.com
2. Rust programming book
3. Install Arch Linux, learn to use the terminal

Cryptography Researcher

Cryptography researchers craft the weapons or implements of change that developers use. They use advanced algebra to exploit the hard limits set by the universe on reality and craft cryptographic schemas that obey certain properties. They are in a sense reality-hackers. They hack reality to create systems that obey objective properties due to the underlying mathematics.

Cryptography researchers create mathematics and repurpose existing algorithms in their schemas. Needless to say, the advanced cryptographer is a good mathematician.

For cryptography, you will study "Abstract Algebra" by Pinter, and starting with simple cryptographic schemes gradually move towards learning more complex ones. You will prototype these schemes using a computer algebra system called SAGE.

Protocol Engineer

Good knowledge of computer science fundamentals as well as the ability to write code. Algebra studies are also required but not to the same degree as cryptography.

The protocol engineer is responsible for blockchain consensus algorithms, developing p2p networks, and other forms of distributed synchronization such as CRDTs. They establish the fundamentals for creating distributed applications and hardening the censorship-resistant properties of crypto. They also harden networks against de-anonymization attempts through the use of encrypted mixnetworking and other techniques.

Protocol engineers have to possess a good knowledge about the theory behind distributed networks, as well as experience in how they work in practice. This topic is part theory, part practical. They must have a good grasp of algorithms and computer science theory.

Other

Alongside this study, continuing to study Ocalan is required. After finishing the Ocalan texts, you can then read Werner's book on economics, as well as Mumford or other philosophers.

Also engagement and familiarization with crypto is a must. Begin following this list and participating in crypto communities.

Starting

1. Download and install a simple Linux operating system to get started. Options can be Ubuntu or Manjaro Linux.
2. Watch Finematics videos.
3. Begin the initial stage listed above.
4. Follow the instructions on the Darkfi Book and run darkirc to connect with the team.

Further Reading

• DarkFi Insights

Current Situation and Macro Overview

• Gensler Vows Action Against DeFi
• Crypto Mega Theses
• The Future of DeFi Must be No KYC
• Every single Bitcoin product banned in the UK as regulators crack down on crypto
• The DOJ’s ‘Crypto Enforcement Framework’ Argues Against Privacy Tools and for International Regulation
• The Coming Storm – Terrorists Using Cryptocurrency
• Report finds $50 billion of cryptocurrency moved out of China hinting at capital flight against Beijing rules

Economics

• mattigag's required reading
• Deribit, On Reflexivity and Imitation, Part 1
  • Part 2
• The Fraying of the US Global Currency Reserve System
• Introduction to Richard Werner: New Paradigm in Marcoeconomics
• Shifting from Central Planning to a Decentralized Economy
• The Great Race to Crypto Banking
• Dreams of a Peasant
• DAO Lay Lo Mo
• Crypto Market Structure

Web 3.0

• Ethereum's Political Philosophy Explained
• Squad Wealth
• Prehistory of DAOs
• Inventories, not Identities
• The origin of the digital antiquities market (NFTs)

Agorism and crypto-anarchy

• How to Return to Crypto's Subversive Roots
• The Crypto Anarchist Manifesto
• Collected Quotations of The Dread Pirate Roberts
• New Libertarian Manifesto
• A Declaration of the Independence of Cyberspace
• A Cypherpunk's Manifesto

rustdoc

Here the rustdoc for this repository's crates can be found.

Libraries

• darkfi
• darkfi-sdk
• darkfi-serial
• darkfi-derive
• darkfi-derive-internal

Binaries

• darkfid
• drk
• fu
• fud
• darkirc
• lilith
• tau
• taud
• vanityaddr
• zkas

Smart contracts

• darkfi-money-contract
• darkfi-dao-contract

Working on native smart contracts

The native network smart contracts are located in src/contract/. Each of the directories contains a Makefile which defines the rules of building the wasm binary, and target for running tests.

The Makefile also contains a clippy target which will perform linting over the webassembly code using the wasm32-unknown-unknown target, and linting over the code (including tests) using RUST_TARGET defined in the Makefile or passed through env.

Developer Seminars

Weekly seminars on DarkFi, cryptography, code and other topics. Each seminar is usually 2 hours long

The link for calls is meet.jit.si/darkfi-seminar.

For the math seminars, we use a collaborative whiteboard called therapy that we made. The canvas will also be shared on Jitsi calls.

Videos will be uploaded online and linked here. Join our chat for more info. Links and text chat will happen there during the calls.

ZK Circuits

Use make bench. For more info, see the Criterion docs.

Verify DAO::vote() Input Proof

Comparison nullifier (red) and SMT (blue)

Desktop

Laptop

Verify DAO::propose() Input Proof

Comparison nullifier (red) and SMT (blue)

Desktop

Laptop

WASM

Times are in micro-seconds. To replicate these tests simply uncomment the line in src/contract/dao/tests/integration.rs which is wallet.bench_wasm = true;. Then do the following lines:

cd src/contract/dao/
make test

Note if you get an error about wasm bincodes not existing, try cd'ing to all directories in the parent, running make in them, then returning back to this directory and repeating the steps again.

Desktop

Laptop

Architecture design

This section of the book shows the software architecture of DarkFi and the network implementations.

For this phase of development we organize into teams lead by a single surgeon. The role of the team is to give full support to the surgeon and make his work effortless and smooth.

Release Cycle

gantt
    title Release Cycle
    dateFormat  DD-MM-YYYY
    axisFormat  %m-%y
    section Phases
    Dcon0            :done, d0, 06-01-2023, 120d
    Dcon1            :done, d1, after d0,   120d
    Dcon2            :done, d2, after d1,   120d
    Dcon3            :done, d3, after d2,   60d
    Dcon4            :      d4, after d3,   14d
    Dcon5            :      d5, after d4,   7d

Mainnet Roadmap

High-level explanations and tasks on the mainnet roadmap, in no particular order. Some may depend on others, use intuition.

DAO Smart Contract

The DAO needs to have a parameter that defines the length of a proposal and the time when it is allowed to vote. Could be a start and end time or just end time. After end time has passed, new votes should be rejected, and only DAO::Exec would be allowed.

The DAO also has to implement ElGamal-ish note encryption in order to be able to be verified inside ZK. darkfi-sdk already provides an interface to this, although not providing an interface to the zkVM, just external. (See ElGamalEncryptedNote in darkfi-sdk). The cryptography also has to be verified for correctness, as this was just a proof of concept.

Smart Contract

Client API:

The native contracts should have a unified and "standard" API so they're all the same. Perhaps it is also possible to define some way for contracts to expose an ABI so it becomes simpler and easier for clients to get the knowledge they need to build transactions and chain contract calls with each other.

Testing Environment:

There is a tool called Zkrunner that takes the zkas circuit and the private inputs, then generates a proof and verify it.

It's like an interactive environment for zkas circuit developer. Without Zkrunner, the developer needs to manually program, and feed the private and pulibc inputs and drive the verification. It needs some code cleanup and documentation on how to use it.

Passive APR/APY

Consensus participants should be incentivised to stake by getting rewards for participation. We need to find something useful for them to do in order to receive these rewards, and also we have to find a way to ensure liveness throughout the entire epoch. The solution to this should not be something that congests the consensus/transaction bandwidth or increases the blockchain size a lot.

Non-native Smart Contract Deployment

There is a basic smart contract called deployooor that is used as a mechanism to deploy arbitrary smart contracts on the network. We need to evaluate the best way to support this. The WASM needs to be verified for correctness (e.g. look through the binary and find if all symbols are in place) so that at least here we disallow people from writing arbitrary data to the chain.

Transaction Fees

TBD

drk

UX!

We need to handle confirmed and unconfirmed transactions, make things prettier and better to use. When broadcasting transactions, if they pass locally, the wallet should be updated to represent the state change but things should stay unconfirmed. The DAO SQL schema gives a nice way to do this, where there's a tx_hash, etc. which can be used to evaluate whether the transaction/coins/whatever was finalized.

We also discussed about having clients handle their own wallets, and not providing a sink through darkfid where there's a single API for interfacing with the wallet, and having to be closely integrated over JSON-RPC <-> SQLite glue. darkfid will only ever have to manage secrets for the consensus coins that are being staked and won't have to deal with the entire wallet itself.

darkirc

Write documentation about usage. We need proper tutorials about running on mobile. Both weechat-android setups, and local ones.

A simple Android app can be made drawing inspiration from Orbot where there is a big On/Off button that can start/stop the node on the phone and then the user can use any IRC client they prefer.

tau

TBD

p2p (anon) git

The motivation is to move off of centralised platforms like Github. Additionally, it would ideally have the capability keep contributor information private.

P2P

The P2P library needs a complete test suite in order to more easily be able to make changes to it without introducing regressions. This includes bad network simulations, latency, etc. The P2P stack also needs to be able to heal itself without restarting the application, much in the way like when you unplug an ethernet cable and then plug it back in. Currently when this happens, all the P2P hosts might be dropped from the known hosts db as they're considered offline/unreachable, so we might want to implement some kind of "quarantine" zone instead of deleting the peers whenever we are unable to connect to them.

In the TLS layer of P2P communication, the client-server certificate logic needs to be reviewed for security and we should define a protocol for this.

zkVM

The zkVM has to implement dynamic self-optimising circuits. The first part and the scaffolding for this is already in place, now we need to come up with an optimisation algorithm that is able to optimally configure the columns used in the circuit based on what the circuit is doing.

All the zkVM opcodes need to be benchmarked for their performance and we need to see how many columns and rows they use so we're able to properly price them for verification fees.

Documentation

• Create beginner level tutorial to introduce contract developement and tools.
• Create a list of outstanding work before mainnet.

Overview

DarkFi is a layer one Proof-of-Work blockchain that supports anonymous applications. It is currently under development. This overview will outline a few key terms that help explain DarkFi.

Blockchain: The DarkFi blockchain is based off Proof of Work RandomX algorithm, paired with Delayed finality. Consensus participating nodes, called miners, produce and propose new blocks to the network, extending some fork chain, which once it reaches a finality security thresshold, can be appended to canonical by all nodes in the network.

Wallet: A wallet is a portal to the DarkFi network. It provides the user with the ability to send and receive anonymous darkened tokens. Each wallet is a full node and stores a copy of the blockchain. All contract execution is done locally on the DarkFi wallet.

P2P Network: The DarkFi ecosystem runs as a network of P2P nodes, where these nodes interact with each other over specific protocols (see node overview). Nodes communicate on a peer-to-peer network, which is also home to tools such as our P2P irc and P2P task manager tau.

ZK smart contracts: Anonymous applications on DarkFi run on proofs that enforce an order of operations. We call these zero-knowledge smart contracts. Anonymous transactions on DarkFi is possible due to the interplay of two contracts, mint and burn (see the sapling payment scheme). Using the same method, we can define advanced applications.

zkas: zkas is the compiler used to compile zk smart contracts in its respective assembly-like language. The "assembly" part was chosen as it's the bare primitives needed for zk proofs, so later on the language can be expanded with higher-level syntax. Zkas enables developers to compile and inspect contracts.

zkVM: DarkFi's zkVM executes the binaries produced by zkas. The zkVM aims to be a general-purpose zkSNARK virtual machine that empowers developers to quickly prototype and debug zk contracts. It uses a trustless zero-knowledge proof system called Halo 2 with no trusted setup.

Anonymous assets

DarkFi network allows for the issuance and transfer of anonymous assets with an arbitrary number of parameters. These tokens are anonymous, relying on zero-knowledge proofs to ensure validity without revealing any other information. All transactions over the network are managed by smart contracts.

New tokens are created and destroyed every time you send an anonymous transaction. To send a transaction on DarkFi, you must first issue a credential that commits to some value you have in your wallet. This is called the Mint phase. Once the credential is spent, it destroys itself: what is called the Burn.

Through this process, the link between inputs and outputs is broken.

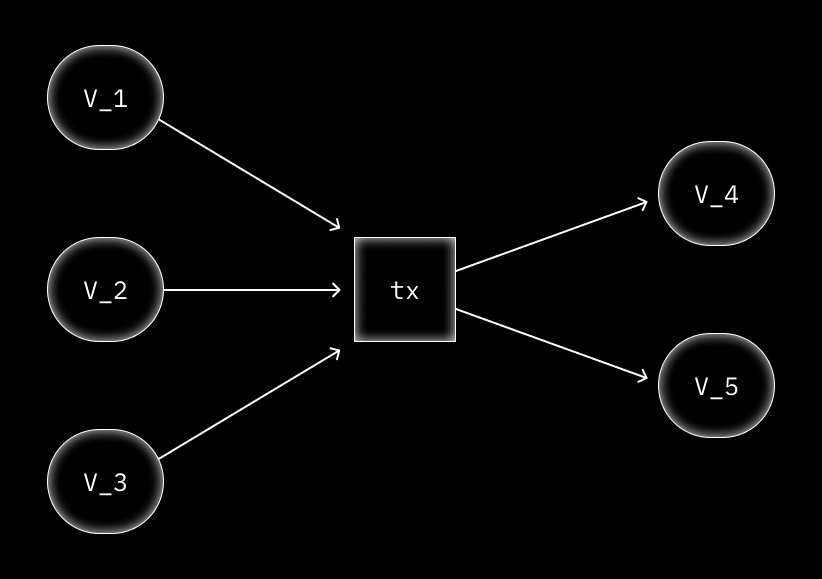
Mint

During the Mint phase we create a new coin commitment $C$, which is bound to the public key $P$. The coin commitment $C$ is publicly revealed on the blockchain and added to the merkle tree, which is stored locally on the DarkFi wallet.

We do this using the following process:

Let $v$ be the coin's value. Generate random $r_C$, $r_V$ and a secret serial $\rho$. The random values ensure the uniqueness and security of the commitment; the serial $\rho$ will be later used to generate the nullifier $N$ of the burn phase and to tie $N$ to $C$.

Create a commitment to these parameters in zero-knowledge:

$$C=H(P,v,\rho ,r_C)$$

Check that the value commitment is constructed correctly:

$$v>0$$ $$V=v{G}_1+r_V{G}_2$$

Reveal $C$ and $V$ commitments. Add $C$ to the Merkle tree.

Burn

When we spend the coin, we must ensure that the value of the coin cannot be double spent. We call this the Burn phase. The process relies on a $N$ nullifier, which we create using the secret key $x$ for the public key $P$ and the coin itself $C$. Nullifiers are unique per coin and prevent double spending. $R$ is the Merkle root. $v$ is the coin's value.

Generate a random number $r_V$.

Check that the secret key corresponds to a public key:

$$P=xG$$

Check that the public key corresponds to a coin which is in the merkle tree $R$:

$$C=H(P,v,\rho ,r_C)$$ $$C\in R$$

Derive the nullifier:

$$N=H(x,C)$$

Check that the value commitment is constructed correctly:

$$v>0$$ $$V=v{G}_1+r_V{G}_2$$

Reveal $N$, $V$ and $R$. Check $R$ is a valid Merkle root. Check $N$ does not exist in the nullifier set.

The zero-knowledge proof confirms that $N$ binds to an unrevealed value $C$, and that this coin is in the Merkle tree, without linking $N$ to $C$. Once the nullifier is produced the coin becomes unspendable.

Adding values

Assets on DarkFi can have any number of values or attributes. This is achieved by creating a credential $C$ and hashing any number of values and checking that they are valid in zero-knowledge.

We check that the sum of the inputs equals the sum of the outputs. This means that:

$$B=\sum V_{in}-\sum V_{out}$$

And that $B$ is a valid point on the curve $G_2$.

This proves that $B=0G_1+b{G}_2=b{G}_2$ where $b$ is a secret blinding factor for the amounts.

Diagram

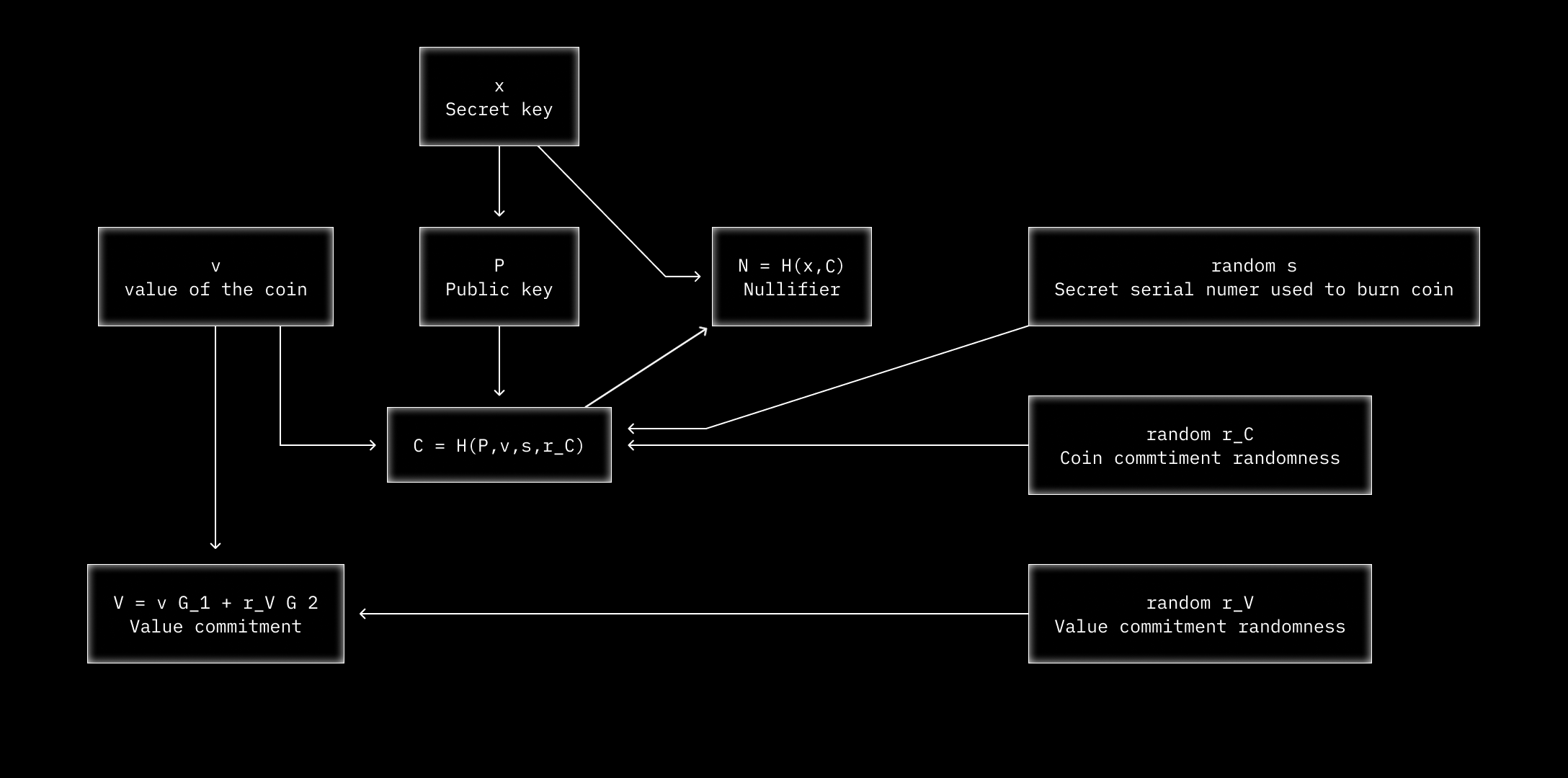
Note: In the diagram $s$ correspond to the $\rho$

Consensus

This section of the book describes how nodes participating in the DarkFi blockchain achieve consensus.

Glossary

Miner main loop

DarkFi uses RandomX Proof of Work algorithm with enforced finality. Therefore, block production involves the following steps:

• First, a miner grabs its current best ranking fork and extends it with a block composed of unproposed transactions from the miner's mempool.

• Then the miner tries to find a nonce such that when the block header is hashed its bytes produce a number that is less than the current difficulty target of the network, using the RandomX mining algorithm.

• Once the miner finds such a nonce, it broadcasts its block proposal to the P2P network. Finally the miner triggers a finalization check to see if its newly extended fork can be finalized.

Pseudocode:

loop {
    fork = find_best_fork()

    block = generate_next_block(fork)

    mine_block(block)

    p2p.broadcast_proposal(block)

    fork.append_proposal(block)

    chain_finalization()
}

Listening for block proposals

Each node listens for new block proposals on the P2P network. Upon receiving block proposals, nodes try to extend the proposals onto a fork held in memory (this process is described in the next section). Then nodes trigger a finalization check to see if their newly extended fork can be finalized.

Upon receiving a new block proposal, miners also check if the extended fork rank is better than the one they are currently trying to extend. If the fork rank is better, the miner will stop mining its proposal and start mining the new best fork.

Ranking

Each block proposal is ranked based on how hard it is to produce. To measure that, we compute the squared distance of its height target from MAX_INT. For two honest nodes that mine the next block height of the highest ranking fork, their block will have the same rank. To mitigate this tie scenario, we also compute the squared distance of the blocks RandomX hash from MAX_INT, allowing us to always chose the actual higher ranking block for that height, in case of ties. The complete block rank is a tuple containing both squared distances.

Proof of Work algorithm lowers the difficulty target as hashpower grows. This means that blocks will have to be mined for a lower target, therefore rank higher, as they go further away from MAX_INT.

Similar to blocks, blockchain/forks rank is a tuple, with the first part being the sum of its block's squared target distances, and the second being the sum of their squared hash distances. Squared distances are used to disproportionately favors smaller targets, with the idea being that it will be harder to trigger a longer reorg between forks. When we compare forks, we first check the first sum, and if its tied, we use the second as the tie breaker, since we know it will be statistically unique for each sequence.

The ranking of a fork is always increasing as new blocks are appended. To see this, let $F=(M_1\cdots M_n)$ be a fork with a finite sequence of blocks $(M_i)$ of length $n$. The rank of a fork is calculated as $$r_F=n\sum _{i=1}^n\text{rank}(M_i)$$ Let $F^{\prime }=F\oplus (M_{n+1})$ of length $n+1$ be the fork created by appending the block $M_{n+1}$ to $F$. Then we see that $$r_{F^{\prime }}>r_F$$ since $\text{rank}(M)>0$ for all $M$.

Fork extension

Since there can be more than one block producer, each node holds a set of known forks in memory. Nodes extend the best ranking fork in memory when producing a block.

Upon receiving a block, one of the following cases may occur:

Visual Examples

Starting state:

               |--[M0] <-- F0
[C]--...--[C]--|
               |--[M1] <-- F1

Blocks on same Y axis have the same height.

Case 1

Extending F0 fork with a new block proposal:

               |--[M0]+--[M2] <-- F0
[C]--...--[C]--|
               |--[M1]        <-- F1

Case 2

Extending F0 fork at [M0] block with a new block proposal, creating a new fork chain:

               |--[M0]--[M2]   <-- F0
[C]--...--[C]--|
               |--[M1]         <-- F1
               |
               |+--[M0]+--[M3] <-- F2

Case 3

Extending the canonical blockchain with a new block proposal:

               |--[M0]--[M2] <-- F0
[C]--...--[C]--|
               |--[M1]       <-- F1
               |
               |--[M0]--[M3] <-- F2
               |
               |+--[M4]      <-- F3

Finalization

Based on the rank properties, each node will diverge to the highest ranking fork, and new fork wil emerge extending that at its tips. A security threshold is set, which refers to the height where the probability to produce a fork, able to reorg the current best ranking fork reaches zero, similar to the # of block confirmation used by other PoW based protocols.

When the finalization check kicks in, each node will grab its best fork. If the fork's length exceeds the security threshold, the node will push (finalize) its first proposal to the canonical blockchain. The fork acts as a queue (buffer) for the to-be-finalized proposals.

Once a finalization occurs, all the fork chains not starting with the finalized block(s) are removed from the node's memory pool.

We continue Case 3 from the previous section to visualize this logic.

The finalization threshold used in this example is 3 blocks. A node observes 2 proposals. One extends the F0 fork and the other extends the F2 fork:

               |--[M0]--[M2]+--[M5] <-- F0
[C]--...--[C]--|
               |--[M1]              <-- F1
               |
               |--[M0]--[M3]+--[M6] <-- F2
               |
               |--[M4]              <-- F3

Later, the node only observes 1 proposal, extending the F2 fork:

               |--[M0]--[M2]--[M5]        <-- F0
[C]--...--[C]--|
               |--[M1]                    <-- F1
               |
               |--[M0]--[M3]--[M6]+--[M7] <-- F2
               |
               |--[M4]                    <-- F3

When the finalization sync period starts, the node finalizes block M0 and keeps the forks that extend that:

               |--[M0]--[M2]--[M5]       <-- F0
[C]--...--[C]--|
               |/--[M1]                  <-- F1
               |
               |--[M0]--[M3]--[M6]--[M7] <-- F2
               |
               |/--[M4]                  <-- F3

The canonical blockchain now contains blocks M0 and the current state is:

               |--[M2]--[M5]       <-- F0
[C]--...--[C]--|
               |--[M3]--[M6]--[M7] <-- F2

Appendix: Data Structures

This section gives further details about the high level structures that will be used by the protocol.

Note that for hashes, we define custom types like TransactionHash, but here we will just use the raw byte representation [u8; 32].

u32 can store 4.29 billion blocks, which with a 90 second blocktime corresponds to 12.2k years.

u16 max value 65535 which is far above the expected limits. By comparison the tx in Bitcoin with the most outputs has 2501.

Header

Block

Blockchain

Fork

Validator

Appendix: Ranking Blocks

Sequences

Denote blocks by the symbols $b_i\in B$, then a sequence of blocks (alternatively a fork) is an ordered series $\mathbf{b}=(b_1,\dots ,b_m)$.

Use $S$ for all sets of sequences for blocks in $B$.

Properties for Rank

Each block is associated with a target $T:B\to \mathbb{I}$ where $\mathbb{I}\subset N$.

1. Blocks with lower targets are harder to create and ranked higher in a sequence of blocks.
2. Given two competing forks $\mathbf{a}=(a_1,\dots ,a_m)$ and $b=(b_1,\dots ,b_n)$, we wish to select a winner. Assume $\mathbf{a}$ is the winner, then $\sum T(a_i)\le \sum T(b_i)$.
3. There should only ever be a single winner. When $\sum T(a_i)=\sum T(b_i)$, then we have logic to break the tie.

Property (2) can also be statistically true for $p>0.5$.

This is used to define a fork-ranking function $W:S\to N$. This function must always have unique values for distinct sequences.

Additivity

We also would like the property $W$ is additive on subsequences $$W((b_1,\dots ,b_m))=W((b_1))+\cdots +W((b_m))$$ which allows comparing forks from any point within the blockchain. For example let $\mathbf{s}=(s_1,\dots ,s_k)$ be the blockchain together with forks $\mathbf{a},\mathbf{b}$ extending $\mathbf{s}$ into $\mathbf{s}\oplus \mathbf{a}=(s_1,\dots ,s_k,a_1,\dots ,a_m)$ and $\mathbf{s}\oplus \mathbf{b}=(s_1,\dots ,s_k,b_1,\dots ,b_n)$. Then we have that $$W(\mathbf{s}\oplus \mathbf{a})<W(\mathbf{s}\oplus \mathbf{b})⟺W(\mathbf{a})<W(\mathbf{b})$$ which means it's sufficient to compare $\mathbf{a}$ and $\mathbf{b}$ directly.

Proposed Rank

With a PoW mining system, we are guaranteed to always have that the block hash $h(b)\le T(b)$. Since the block hashes $(h(b_1),\dots ,h(b_m))$ for a sequence $(b_1,\dots ,b_m)$ have the property that $\sum h(b_i)\le \sum T(b_i)$, as well as being sufficiently random, we can use them to define our work function.

Because $W$ is required to be additive, we define a block work function $w:B\to N$, and $W(\mathbf{b})=\sum w(b_i)$.

The block work function should have a statistically higher score for blocks with a smaller target, and always be distinct for unique blocks. We define $w$ as $$w(b)=\text{max}(\mathbb{I})-h(b)$$ since $h(b)<T(b)<\text{max}(\mathbb{I})$ this function is well defined on the codomain.

Hash Function

Let $\mathbb{I}$ be a fixed subset of $N$ representing the output of a hash function $[0,\text{max}(\mathbb{I})]$.

Definition: a hash function is a function $H:N\to \mathbb{I}$ having the following properties:

1. Uniformity, for any $y\in \mathbb{I}$ and any $n\in N$, there exists an $N>n$ such that $H(N)=y$.
2. One-way, for any $y\in \mathbb{I}$, we are unable to construct an $x\in N$ such that $H(x)=y$.

Note: the above notions rely on purely algebraic properties of $H$ without requiring the machinery of probability. The second property of being one-way is a stronger notion than $\text{ran}(H)$ being statistically random. Indeed if the probability is non-zero then we could find such an $(x,y)$ which breaks the one-way property.

Theorem: given a hash function $H:N\to \mathbb{I}$ as defined above, it's impossible to construct two distinct sequences $\mathbf{a}=(a_1,\dots ,a_m)$ and $\mathbf{b}=(b_1,\dots ,b_n)$ such that $H(a_1)+\cdots +H(a_m)=H(b_1)+\cdots +H(b_n)$.

By property (2), we cannot find a $H(x)=0$. Again by (2), we cannot construct an $x$ such that $H(x)+H(a)=H(b)$ for any $a,b\in N$. Recursive application of (2) leads us to the stated theorem.

Transactions

(Temporary document, to be integrated into other docs)

Transaction behaviour

In our network context, we have two types of nodes.

1. Miner (M)
2. Spectator (S)

S acts as a relayer for transactions in order to help out that transactions reach M.

To avoid spam attacks, S should keep $tx$ in their mempool for some period of time, and then prune it.

Ideal simulation with instant finality

The lifetime of a transaction $tx$ that passes verification and whose state transition can be applied on top of the finalized (canonical) chain:

1. User creates a transaction $tx$
2. User broadcasts $tx$ to S
3. S validates $tx$ state transition
4. $tx$ enters S mempool
5. S broadcasts $tx$ to M
6. M validates $tx$ state transition
7. $tx$ enters M mempool
8. M validates all transactions in its mempool in sequence
9. M proposes a block finalization containing $tx$
10. M writes the state transition update of $tx$ to their chain
11. M removes $tx$ from their mempool
12. M broadcasts the finalized proposal
13. S receives the proposal and validates transactions
14. S writes the state updates to their chain
15. S removes $tx$ from their mempool

Real-world simulation with non-instant finality

The lifetime of a transaction $tx$ that passes verification and whose state transition is pending to be applied on top of the finalized (canonical) chain:

1. User creates a transaction $tx$
2. User broadcasts $tx$ to S
3. S validates $tx$ state transition
4. $tx$ enters S mempool
5. S broadcasts $tx$ to M
6. M validates $tx$ state transition
7. $tx$ enters M mempool
8. M proposes a block proposal containing $tx$
9. M proposes more block proposals
10. When proposals can be finalized, M validates all their transactions in sequence
11. M writes the state transition update of $tx$ to their chain
12. M removes $tx$ from their mempool
13. M broadcasts the finalized proposals sequence
14. S receives the proposals sequence and validates transactions
15. S writes the state updates to their chain
16. S removes $tx$ from their mempool

Real-world simulation with non-instant finality, forks and multiple CP nodes

The lifetime of a transaction $tx$ that passes verifications and whose state transition is pending to be applied on top of the finalized (canonical) chain:

1. User creates a transaction $tx$
2. User broadcasts $tx$ to S
3. S validates $tx$ state transition against canonical chain state
4. $tx$ enters S mempool
5. S broadcasts $tx$ to P
6. M validates $tx$ state transition against all known fork states
7. $tx$ enters M mempool
8. M broadcasts $tx$ to rest M nodes
9. Block producer SM finds which fork to extend
10. SM validates all unproposed transactions in its mempool in sequence, against extended fork state, discarding invalid
11. SM creates a block proposal containing $tx$ extending the fork
12. M receives block proposal and validates its transactions against the extended fork state
13. SM proposes more block proposals extending a fork state
14. When a fork can be finalized, M validates all its proposals transactions in sequence, against canonical state
15. M writes the state transition update of $tx$ to their chain
16. M removes $tx$ from their mempool
17. M drop rest forks and keeps only the finalized one
18. M broadcasts the finalized proposals sequence
19. S receives the proposals sequence and validates transactions
20. S writes the state updates to their chain
21. S removes $tx$ from their mempool

M will keep $tx$ in its mempool as long as it is a valid state transition for any fork(including canonical) or it get finalized.

Unproposed transactions refers to all $tx$ not included in a proposal of any fork.

If a fork that can be finalized fails to validate all its transactions(14), it should be dropped.

The Transaction object

pub struct ContractCall {
    /// The contract ID to which the payload is fed to
    pub contract_id: ContractId,
    /// Arbitrary payload for the contract call
    pub payload: Vec<u8>,
}

pub struct Transaction {
    /// Calls executed in this transaction
    pub calls: Vec<ContractCall>,
    /// Attached ZK proofs
    pub proofs: Vec<Vec<Proof>>,
    /// Attached Schnorr signatures
    pub signatures: Vec<Vec<Signature>>,
}

A generic DarkFi transaction object is simply an array of smart contract calls, along with attached ZK proofs and signatures needed to properly verify the contracts' execution. A transaction can have any number of calls, and proofs, provided it does not exhaust a set gas limit.

In DarkFi, every operation is a smart contract. This includes payments, which we'll explain in the following section.

Payments

For A -> B payments in DarkFi we use the Sapling scheme that originates from zcash. A payment transaction has a number of inputs (which are coins being burned/spent), and a number of outputs (which are coins being minted/created). An explanation for the ZK proofs for this scheme can be found in the Zkas section of this book, under Sapling.

In code, the structs we use are the following:

pub struct MoneyTransferParams {
    pub inputs: Vec<Input>,
    pub outputs: Vec<Output>,
}

pub struct Input {
    /// Pedersen commitment for the input's value
    pub value_commit: ValueCommit,
    /// Pedersen commitment for the input's token ID
    pub token_commit: ValueCommit,
    /// Revealed nullifier
    pub nullifier: Nullifier,
    /// Revealed Merkle root
    pub merkle_root: MerkleNode,
    /// Public key for the Schnorr signature
    pub signature_public: PublicKey,
}

pub struct Output {
    /// Pedersen commitment for the output's value
    pub value_commit: ValueCommit,
    /// Pedersen commitment for the output's token ID
    pub token_commit: ValueCommit,
    /// Minted coin: poseidon_hash(pubkey, value, token, serial, blind)
    pub coin: Coin,
    /// The encrypted note ciphertext
    pub encrypted_note: EncryptedNote,
}

pub struct EncryptedNote {
    pub ciphertext: Vec<u8>,
    pub ephemeral_key: PublicKey,
}

pub struct Note {
    /// Serial number of the coin, used to derive the nullifier
    pub serial: pallas::Base,
    /// Value of the coin
    pub value: u64,
    /// Token ID of the coin
    pub token_id: TokenId,
    /// Blinding factor for the value Pedersen commitment
    pub value_blind: ValueBlind,
    /// Blinding factor for the token ID Pedersen commitment
    pub token_blind: ValueBlind,
    /// Attached memo (arbitrary data)
    pub memo: Vec<u8>,
}

In the blockchain state, every minted coin must be added into a Merkle tree of all existing coins. Once added, the new tree root is used to prove existence of this coin when it's being spent.

Let's imagine a scenario where Alice has 100 ALICE tokens and wants to send them to Bob. Alice would create an Input object using the info she has of her coin. She has to derive a nullifier given her secret key and the serial number of the coin, hash the coin bulla so she can create a merkle path proof, and derive the value and token commitments using the blinds.

let nullifier = poseidon_hash([alice_secret_key, serial]);
let signature_public = alice_secret_key * Generator;
let coin = poseidon_hash([signature_public, value, token_id, blind]);
let merkle_root = calculate_merkle_root(coin);
let value_commit = pedersen_commitment(value, value_blind);
let token_commit = pedersen_commitment(token_id, token_blind);

The values above, except coin become the public inputs for the Burn ZK proof. If everything is correct, this allows Alice to spend her coin. In DarkFi, the changes have to be atomic, so any payment transaction that is burning some coins, has to mint new coins at the same time, and no value must be lost, nor can the token ID change. We enforce this by using Pedersen commitments.

Now that Alice has a valid Burn proof and can spend her coin, she can mint a new coin for Bob.

let blind = pallas::Base::random();
let value_blind = ValueBlind::random();
let token_blind = ValueBlind::random();
let coin = poseidon_hash([bob_public, value, token_id, blind]);
let value_commit = pedersen_commitment(value, value_blind);
let token_commit = pedersen_commitment(token, token_blind);

coin, value_commit, and token_commit become the public inputs for the Mint ZK proof. If this proof is valid, it creates a new coin for Bob with the given parameters. Additionally, Alice would put the values and blinds in a Note which is encrypted with Bob's public key so only Bob is able to decrypt it. This Note has the necessary info for him to further spend the coin he received.

At this point Alice should have 1 input and 1 output. The input is the coin she burned, and the output is the coin she minted for Bob. Along with this, she has two ZK proofs that prove creation of the input and output. Now she can build a transaction object, and then use her secret key she derived in the Burn proof to sign the transaction and publish it to the blockchain.

The blockchain will execute the smart contract with the given payload and verify that the Pedersen commitments match, that the nullifier has not been published before, and also that the merkle authentication path is valid and therefore the coin existed in a previous state. Outside of the VM, the validator will also verify the signature(s) and the ZK proofs. If this is valid, then Alice's coin is now burned and cannot be used anymore. And since Alice also created an output for Bob, this new coin is now added to the Merkle tree and is able to be spent by him. Effectively this means that Alice has sent her tokens to Bob.

Anonymous Bridge (DRAFT)

We present an overview of a possibility to develop anonymous bridges from any blockchain network that has tokens/balances on some address owned by a secret key. Usually in networks, we have a secret key which we use to derive a public key (address) and use this address to receive funds. In this overview, we'll go through such an operation on the Ethereum network and see how we can bridge funds from ETH to DarkFi.

Preliminaries

Verifiable secret sharing¹

Verifiable secret sharing ensures that even if the dealer is malicious there is a well-defined secret that the players can later reconstruct. VSS is defined as a secure multi-party protocol for computing the randomized functionality corresponding to some secret sharing scheme.

Secure multiparty computation²

Multiparty computation is typically accomplished by making secret shares of the inputs, and manipulating the shares to compute some function. To handle "active" adversaries (that is, adversaries that corrupt nodes and make them deviate from the protocol), the secret sharing scheme needs to be verifiable to prevent the deviating nodes from throwing off the protocol.

General bridge flow

Assume Alice wants to bridge 10 ETH from the Ethereum network into DarkFi. Alice would issue a bridging request and perform a VSS scheme with a network of nodes in order to create an Ethereum secret key, and with it - derive an Ethereum address. Using such a scheme should prevent any single party to retrieve the secret key and steal funds. This also means, for every bridging operation, a fresh and unused Ethereum address is generated and as such gives no convenient ways of tracing bridge deposits.

Once the new address has been generated, Alice can now send funds to the address and either create some proof of deposit, or there can be an oracle that verifies the state on Ethereum in order to confirm that the funds have actually been sent.

Once confirmed, the bridging smart contract is able to freshly mint the counterpart of the deposited funds on a DarkFi address of Alice's choice.

Open questions:

• What to do with the deposited funds?

It is possible to send them to some pool or smart contract on ETH, but this becomes an address that can be blacklisted as adversaries can assume it is the bridge's funds. Alternatively, it could be sent into an L2 such as Aztec in order to anonymise the funds, but (for now) this also limits the variety of tokens that can be bridged (ETH & DAI).

• How to handle network fees?

In the case where the token being bridged cannot be used to pay network fees (e.g. bridging DAI from ETH), there needs to be a way to cover the transaction costs. The bridge nodes could fund this themselves but then there also needs to be some protection mechanism to avoid people being able to drain those wallets from their ETH.

Tooling

DarkFi Fullnode Daemon

darkfid is the darkfi fullnode. It manages the blockchain, validates transactions and remains connected to the p2p network.

Clients can connect over localhost RPC or secure socket and perform these functions:

• Get the node status and modify settings realtime.
• Query the blockchain.
• Broadcast txs to the p2p network.
• Get tx status, query the mempool and interact with components.

darkfid does not have any concept of keys or wallet functionality. It does not manage keys.

Low Level Client

Clients manage keys and objects. They make queries to darkfid, and receive notes encrypted to their public keys.

Their design is usually specific to their application but modular.

They also expose a high level simple to use API corresponding exactly to their commands so that product teams can easily build an application. They will use the command line tool as an interactive debugging application and point of reference.

The API should be well documented with all arguments explained. Likewise for the commands help text.

Command cheatsheets and example sessions are strongly encouraged.

P2P Network

We instantiate a p2p network and call start(). This will begin running a single p2p network until stop() is called.

There are 3 session types:

• InboundSession, concerned with incoming connections
• OutboundSession, concerned with outgoing connections
• SeedSession is a special session type which connects to seed nodes to populate the hosts pool, then finishes once synced.

Connections are made by either Acceptor or Connector for incoming or outgoing respectively. They have multiple transport types; see src/net/transport/ for the full list.

Connections are then wrapped in a Channel abstraction which allows protocols to be attached. See src/net/protocol/ and run fd protocol for custom application specific network protocols. Also see the follow tutorial:

• Understanding Protocols

Outbound Session

The outbound session is responsible to ensure the hosts pool is populated, either through currently connected nodes or using the seed session. It performs this algorithm:

1. Start $N$ slots, and a sleeping peer discovery process

Then each slot performs this algorithm:

1. If no addresses matching our filters are in the hosts pool then:
   1. Wakeup the peer discovery process. This does nothing if peer discovery is already active.
   2. Peer discovery tries first 2 times to poll the current network if there are connected nodes, otherwise it will do a seed server sync.
   3. Peer discovery then wakes any sleeping slots and goes back to sleep.

Hostlist filtering

Node maintain a hostlist consisting of three parts, a whitelist, a greylist and an anchorlist. Each hostlist entry is a tuple of two parts, a URL address and a last_seen data field, which is a timestamp of the last time the peer was interacted with.

The lists are ordered chronologically according to last_seen, with the most recently seen peers at the top of the list. The whitelist max size is 1000. The greylist max size is 5000. If the number of peers in these lists reach this maximum, then the peers with the oldest last_seen fields are removed from the list.

Each time a node receives info about a set of peers, the info is inserted into its greylist. To discover peers, nodes broadcast GetAddr messages. Upon receiving a GetAddr message, peers reply with an Addr message containing their whitelist. The requester inserts the received peer data into its greylist.

Nodes update their hostlists through a mechanism called "greylist housekeeping", which periodically pings randomly selected peers from its greylist. If a peer is responsive, then it is promoted to the whitelist with an updated last_seen field, otherwise it is removed from the greylist.

On shutdown, whitelist entries are downgraded to greylist. This forces all whitelisted entries through the greylist refinery each time a node is started, further ensuring that whitelisted entries are active.

If a connection is established to a host, that host is promoted to anchorlist. If anchorlist or whitelist nodes disconnect or cannot be connected to, those hosts are downgraded to greylist.

Nodes can configure how many anchorlist connections or what percentage of whitelist connections they would like to make, and this configuration influences the connection behavior in OutboundSession. If there's not enough anchorlist entries, the connection loop will select from the whitelist. If there's not enough whitelist entries in the hostlist, it will select from the greylist.

This design has been largely informed by the Monero p2p algo

Security

Design Considerations

• Mitigate attacks to a reasonable degree. Ensuring complete coverage against attacks is infeasible and likely introduces significant latency into protocols.
• Primarily target the p2p network running over anonymity networks like Tor, i2p or Nym. This means we cannot rely on node addresses being reliable. Even on the clearnet, attackers can easily obtain large numbers of proxy addresses.

The main attacks are:

• Sybil attack. A malicious actor tries to subvert the network using sockpuppet nodes. For example false signalling using version messages on the p2p network.
• Eclipse attack. Targets a single node, through a p2p MitM attack where the malicious actor controls all the traffic you see. For example they might send you a payment, then want to doublespend without you knowing about it.
• Denial of Service. Usually happens when a node is overloaded by too much data being sent.

Common Mitigations

• Backoff/falloff. This is the strategy implemented in Bitcoin. This can be bad when arbitrary limits are implemented since we slow down traffic for no reason.
• Choking controller. BitTorrent no longer uses naive tit-for-tat, instead libtorrent implements an anti-leech seeding algo from the paper Improving BitTorrent: A Simple Approach, which is focused on distributing bandwidth to all peers. See also libtorrent/src/choker.cpp.
  • All p2p messages will have a score which represents workload for the node. There is a hard limit, and in general the choker will try to balance the scores between all available channels.
  • Opening the connection itself has a score with inbound connections assigned more cost than outgoing ones.
• Smart ban. Malicious peers which violate protocols are hard banned. For example sending the wrong data for a chunk.
  • See the method channel.ban() which immediately disconnects and blacklists the address.
• uTP congestion control. BitTorrent implements a UDP protocol with its own congestion control. We could do such a similar strategy with the addition of removing ordering. This reduces protocol latency mitigating attacks. See libtorrent.org/utp.html for more info.
  • Maybe less important if we use alternative networks like Tor or i2p.
• White, gray and black lists. See section 2.2 of Exploring the Monero P2P Network for details of this algorithm. This aids with network connectivity, avoiding netsplits which could make the network more susceptible to eclipse/sybil attacks (large scale MiTM).
  • See: Refine Session
• Protocol-level reputation system. You have a keypair, which accrues more trust from the network. Nodes gossip trust metrics.
  • See AnonRep: Towards Tracking-Resistant Anonymous Reputation
  • Also the discussion in Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting
• Reduce blast radius. The p2p subsystem should run on its own dedicated executor, separate from database lookups or other system operations.
• fail2ban
• Optimized blockchain database. Most databases are written for interleaved reads and writes as well as deletion. Blockchains follow a different pattern of infrequent writes being mostly append-only, and requiring weaker guarantees.

Protocol Suggestions

Core protocols should be modeled and analyzed with DoS protections added. Below are suggestions to start the investigation.

• Do not forward orphan txs or blocks.
• Drop all double spend txs.
  • Alternatively require a higher fee if we want to enable replace by fee.
  • Do not forward double spend txs.
• Do not forward the same object (block, transaction .etc) to the same peer twice. Violation results in channel.ban().
• Very low fee txs are rate limited.
• Limit orphan txs.
• Drop large or unusual orphan transactions to limit damage.
• Consider a verification cache to prevent attacks that try to trigger re-verification of stored orphan txs. Also limit the size of the cache. See Fixed vulnerability explanation: Why the signature cache is a DoS protection.
• Perform more expensive checks later in tx validation.
• Nodes will only relay valid transactions with a certain fee amount. More expensive transactions require a higher fee.
• Complex operations such as requesting data can be mitigated by tracking the number of requests from a peer.
  • Attackers may attempt flooding invs for invalid data. The peer responds with get data but that object doesn't exist using up precious bandwidth. Limit both the rate of invs to 2/s and size of items to 35.
  • Also loops can cause an issue if triggered by the network. This should be carefully analyzed and flattened if possible, otherwise they should be guarded against attack.

Customizable Policy

Apps should be able to configure:

• Reject hosts, for example based off current overall resource utilization or the host addr.
  • Note: we have a configurable setting called blacklist which allows us to reject hosts by addr.
• Accounting abstraction for scoring connections.

Swarming

TODO: research how this is handled on bittorrent. How do we lookup nodes in the swarm? Does the network maintain routing tables? Is this done through a DHT like Kademlia?

Swarming means more efficient downloading of data specific to a certain subset. A new p2p instance is spawned with a clean hosts table. This subnetwork is self contained.

An application is for example DarkIRC where everyday a new event graph is spawned. With swarming, you would connect to nodes maintaining this particular day's event graph.

The feature allows overlaying multiple different features in a single network such as tau, darkirc and so on. New networks require nodes to bootstrap, but with swarming, we reduce all these networks to a single bootstrap. The overlay network maintaining the routing tables is a kind of decentralized lilith which keeps track of all the swarms.

Possibly a post-mainnet feature depending on the scale of architectural changes or new code required in the net submodule.

To faciliate this future upgrade, we have made the peer discovery process a generic trait called PeerDiscoveryBase. Currently there is only one imeplementation, PeerDiscovery, which implements the peer discovery process in outbound sesssion. In the future PeerDiscoveryBase can be implemented to make new forms of peer discovery (i.e. subnets vs overlay peer discovery processes).

Scoring Subsystem

Connections should maintain a scoring system. Protocols can increment the score.

The score backs off exponentially. If the watermark is crossed then the connection is dropped.

Since the reader in messages.rs preallocs buffers, there should be a hard limit here, and the raw reads also affects your score too.

Services

Nodes and applications are composed out of services. These are long running components that may communicate with each other.

The standard signature for a service is of the form:

use darkfi::ExecutorPtr;

pub struct Service {
    // ...
}

impl Service {
    pub fn new(/* ... */, executor: ExecutorPtr) -> Arc<Self> {
        // ...
    }

    pub async fn start(self: Arc<Self>) {
        // ...
    }

    pub async fn stop(&self) {
    }
}

Both start() and stop() should return immediately without blocking the caller. Any long running tasks they need to perform should be done using StoppableTask (see below).

StoppableTask

Services will likely want to start any number of processes. For that you can use StoppableTask.

For example ManualSession looks like this:

pub struct ManualSession {
    p2p: Weak<P2p>,
    connect_slots: Mutex<Vec<StoppableTaskPtr>>,
    // ...
}

impl ManualSession {
    pub fn new(p2p: Weak<P2p>) -> ManualSessionPtr {
        Arc::new(Self {
            p2p,
            connect_slots: Mutex::new(Vec::new()),
            // ...
        })
    }

    pub async fn connect(self: Arc<Self>, addr: Url) {
        let ex = self.p2p().executor();
        let task = StoppableTask::new();

        task.clone().start(
            self.clone().channel_connect_loop(addr),
            // Ignore stop handler
            |_| async {},
            Error::NetworkServiceStopped,
            ex,
        );

        self.connect_slots.lock().await.push(task);
    }

    pub async fn stop(&self) {
        let connect_slots = &*self.connect_slots.lock().await;

        for slot in connect_slots {
            slot.stop().await;
        }
    }
    
    // ...
}

The method in start() is a future that returns Result<()>. If you do not want to return a result (for example with long running processes), then simply use the future:

    async {
        foo().await;
        unreachable!()
    }

Communicating Between Services

Another tool in our toolbox is the subscribe()/notify() paradigm.

We can use system::Subscriber. Then inside our method we can define a method like so:

    pub async fn subscribe_stop(&self) -> Result<Subscription<Error>> {
        let sub = self.stop_subscriber.clone().subscribe().await;
        Ok(sub)
    }

    // ...

    // Invoke it like this
    self.stop_subscriber.notify(Error::ChannelStopped).await;

Then the API user can simply do:

let stop_sub = channel.subscribe_stop().await?;
let err = stop_sub.receive().await;
stop_sub.unsubscribe().await;

Parent-Child Relationships

In the async context we are forced to use Arc<Self>, but often times we want a parent-child relationship where if both parties contain an Arc reference to the other it creates a circular loop. For this case, there is a handy helper called LazyWeak.

pub struct Parent {
    child: Arc<Child>,
    // ...
}

impl Parent {
    pub async fn new(/* ... */) -> Arc<Self> {
        let self_ = Arc::new(Self {
            child: Child::new(),
            // ...
        });

        self_.child.parent.init(self_.clone());
        // ...
        self_
    }

    // ...
}


pub struct Child {
    pub parent: LazyWeak<Parent>,
    // ...
}

impl Child {
    pub fn new() -> Arc<Self> {
        Arc::new(Self {
            parent: LazyWeak::new(),
            // ...
        })
    }

    // ...
}

Otherwise if the relationship is just one way, use Arc<Foo>. For example if doing dependency injection where component B dependent on component A, then we could do:

let comp_a = Foo::new();
let comp_b = Bar::new(comp_a);

Anonymous Smart Contracts

• Important Invariants
• Global Smart Contract State
• Atomic Transactions
• ZK Proofs and Signatures
• Invoking Contracts
  • Depending on State Changes
• ABI
• Events

Every full node is a verifier.

Prover is the person executing the smart contract function on their secret witness data. They are also verifiers in our model.

Lets take a pseudocode smart contract:

contract Dao {
    # 1: the DAO's global state
    dao_bullas = DaoBulla[]
    proposal_bullas = ProposalBulla[]
    proposal_nulls = ProposalNull[]

    # 2. a public smart contract function
    #    there can be many of these
    fn mint(...) {
        ...
    }

    ...
}

Important Invariants

1. The state of a contract (the contract member values) is globally readable but only writable by that contract's functions.
2. Transactions are atomic. If a subsequent contract function call fails then the earlier ones are also invalid. The entire tx will be rolled back.
3. foo_contract::bar_func::validate::process() is able to access the entire transaction to perform validation on its structure. It might need to enforce requirements on the calldata of other function calls within the same tx. See DAO::exec().

Global Smart Contract State

Internally we could represent this smart contract like this:

mod dao_contract {
    // Corresponds to 2. mint()
    // Prover specific
    struct MintCall {
        ...
        // secret witness values for prover
        ...
    }

    impl MintCall {
        fn new(...) -> Self {
            ...
        }

        fn make() -> FuncCall {
            ...
        }
    }

    // Verifier code
    struct MintParams {
        ...
        // contains the function call data
        ...
    }
}

There is a pipeline where the prover runs MintCall::make() to create the MintParams object that is then broadcast to the verifiers through the p2p network.

The CallData usually is the public values exported from a ZK proof. Essentially it is the data used by the verifier to check the function call for DAO::mint().

Atomic Transactions

Transactions represent several function call invocations that are atomic. If any function call fails, the entire tx is rejected. Additionally some smart contracts might impose additional conditions on the transaction's structure or other function calls (such as their call data).

/// A Transaction contains an arbitrary number of `ContractCall` objects,
/// along with corresponding ZK proofs and Schnorr signatures. `DarkLeaf`
/// is used to map relations between contract calls in the transaction.
#[derive(Clone, Default, Eq, PartialEq, SerialEncodable, SerialDecodable)]
pub struct Transaction {
    /// Calls executed in this transaction
    pub calls: Vec<DarkLeaf<ContractCall>>,
    /// Attached ZK proofs
    pub proofs: Vec<Vec<Proof>>,
    /// Attached Schnorr signatures
    pub signatures: Vec<Vec<Signature>>,
}

Function calls represent mutations of the current active state to a new state.

/// A ContractCall is the part of a transaction that executes a certain
/// `contract_id` with `data` as the call's payload.
#[derive(Clone, Eq, PartialEq, SerialEncodable, SerialDecodable)]
pub struct ContractCall {
    /// ID of the contract invoked
    pub contract_id: ContractId,
    /// Call data passed to the contract
    pub data: Vec<u8>,
}

The contract_id corresponds to the top level module for the contract which includes the global State.

The func_id of a function call corresponds to predefined objects in the submodules:

• Builder creates the anonymized CallData. Ran by the prover.
• CallData is the parameters used by the anonymized function call invocation. Verifiers have this.
• process() that runs the function call on the current state using the CallData.
• apply() commits the update to the current state taking it to the next state.

An example of a contract_id could represent DAO or Money. Examples of func_id could represent DAO::mint() or Money::transfer().

Each function call invocation is ran using its own process() function.

mod dao_contract {
    ...

    // DAO::mint() in the smart contract pseudocode
    mod mint {
        ...

        fn process(states: &StateRegistry, func_call_index: usize, parent_tx: &Transaction) -> Result<Update> {
            // we could also change the process() function signature
            // so we pass the func_call itself in
            let func_call = parent_tx.func_calls[func_call_index];
            let call_data = func_call.call_data;
            // It's useful to have the func_call_index within parent_tx because
            // we might want to enforce that it appears at a certain index exactly.
            // So we know the tx is well formed.

            ...
        }
    }
}

process() has access to the entire atomic transaction to enforce correctness. For example combining of function calls is used by the DAO::exec() smart contract function to execute moving money out of the treasury using Money::transfer() within the same transaction.

Additionally smart contracts have access to the global states of all smart contracts on the network, which is needed for some contracts.

Note that during this step, the state is not modified. Modification happens after the process() is run for all function call invocations within the transaction. Assuming they all pass successfully, the updates are then applied at the end. This ensures atomicity property of transactions.

mod dao_contract {
    ...

    // DAO::mint() in the smart contract pseudocode
    mod mint {
        ...

        // StateRegistry is mutable
        fn apply(states: &mut StateRegistry, update: Update) {
            ...
        }
    }
}

The transaction verification pipeline roughly looks like this:

1. Loop through all function call invocations within the transaction:
   1. Lookup their respective process() function based off their contract_id. The contract_id and func_id corresponds to the contract and specific function, such as DAO::mint().
   2. Call the process() function and store the update. Halt if this function fails.
2. Loop through all updates
   1. Lookup specific apply() function based off the contract_id and func_id.
   2. Call apply(update) to finalize the change.

ZK Proofs and Signatures

Lets review again the format of transactions.

/// A Transaction contains an arbitrary number of `ContractCall` objects,
/// along with corresponding ZK proofs and Schnorr signatures. `DarkLeaf`
/// is used to map relations between contract calls in the transaction.
#[derive(Clone, Default, Eq, PartialEq, SerialEncodable, SerialDecodable)]
pub struct Transaction {
    /// Calls executed in this transaction
    pub calls: Vec<DarkLeaf<ContractCall>>,
    /// Attached ZK proofs
    pub proofs: Vec<Vec<Proof>>,
    /// Attached Schnorr signatures
    pub signatures: Vec<Vec<Signature>>,
}

And corresponding function calls.

/// A ContractCall is the part of a transaction that executes a certain
/// `contract_id` with `data` as the call's payload.
#[derive(Clone, Eq, PartialEq, SerialEncodable, SerialDecodable)]
pub struct ContractCall {
    /// ID of the contract invoked
    pub contract_id: ContractId,
    /// Call data passed to the contract
    pub data: Vec<u8>,
}

As we can see the ZK proofs and signatures are separate from the actual call_data interpreted by process(). They are both automatically verified by the VM.

However for verification to work, the ZK proofs also need corresponding public values, and the signatures need the public keys. We do this by exporting these values. (TODO: link the code where this happens)

These methods export the required values needed for the ZK proofs and signature verification from the actual call data itself.

For signature verification, the data we are verifying is simply the entire transactions minus the actual signatures. That's why the signatures are a separate top level field in the transaction.

This section of the book documents smart contract development.

Invoking Contracts

In Solana and Ethereum, when invoking a contract, the call happens directly at the site of calling. That means the calling contract is responsible for constructing the params used to process the instruction.

In our case, it's more complicated since a smart contract function invocation involves ZK proofs with get_metadata() that can be verified in parallel. If we used the above model, we would first have to execute process() before verifying the proofs or signatures.

Also arbitrary invocation allows arbitrary infinite recursion.

The alternative method which is close to what we're doing already, is having the entire callgraph as a tree. Each ContractCall, now has a field called children: Vec<ContractCall>.

pub struct ContractCall {
    /// ID of the contract invoked
    pub contract_id: ContractId,
    /// Call data passed to the contract
    pub data: Vec<u8>,

    /// Contract calls invoked by this one
    pub children: Vec<ContractCall>,
}

Let n = len(children). Then inside the contract, we are expected to call invoke() exactly n times.

    let (params, retdat) = invoke(function_id);

This doesn't actually invoke any function directly, but just iterates to the next child call in the current call. We should iterate through the entire list. If this doesn't happen, then there's a mismatch and the call fails with an error.

This logic is handled completely inside the contract without needing host functions.

The downside is that the entire calldata for a smart contract is bundled in a tx, and isn't generated on the fly. This makes tx size bigger. However since we need ZK proofs, I expect the calldata would need to bundle the proofs for all invoked calls anyway.

Essentially the entire program trace is created ahead of time by the "prover", and then the verifier simply checks the trace for correctness. This can be done in parallel since we have all the data ahead of time.

Depending on State Changes

Another downside of this model is that state changes at the site of invocation are not immediate.

Currently in DarkFi, we separate contract calls into 2-phases: process() which verifies the calldata, and update() which takes a state update from process() and writes the changes.

Host functions have permissions:

• process() is READONLY, which means state can only be read. For example it can use db_get() but not db_set().
• update() is WRITEONLY. It can only write to the state. For example it can use db_set() but not db_get().

Let A, B be smart contract functions. A calls invoke(B). The normal flow in Ethereum would be:

process(A) ->
    invoke(B) ->
        process(B) ->
        update(B) ->
update(A)

However with the model described, instead would be:

process(B) ->
update(B) ->
process(A) ->
update(A)

which simulates the previous trace.

State changes occur linearly after all process() calls have passed successfully.

NOTE: we can iterate depth first through the tree to simulate the normal calling pattern.

An upside of this strict separation, is that it makes reentrancy attacks impossible. Say for example we have this code:

contract VulnerableContract {
    function withdraw(amount) {
        // ...
        sender.call(amount);
        balances[sender] -= amount;
    }
}

contract AttackerContract {
    function receive(amount) {
        if balance(VulnerableContract) >= 1 {
            VulnerableContract.withdraw(1);
        }
    }
}

The main recommended way to mitigate these attacks is using the 'checks-effects-interactions' pattern[1] [2]. whereby the code is delineated into 3 strict parts.

contract ChecksEffectsInteractions {
    // ...

    function withdraw(uint amount) public {
        require(balances[msg.sender] >= amount);

        balances[msg.sender] -= amount;

        msg.sender.transfer(amount);
    }
}

Interactions always occur last since they cause unknown effects. Performing logic based off state changes from an interacting outside contract (especially when user provided) is very risky.

With the model of invoke() given above, we do not have any possibility of such an attack occurring.

ABI

We can do this in Rust through clever use of the serializer. Basically there is a special overlay provided for a Model which describes its layout. The layout saves the field names and types. Later this can be provided via a macro.

Then dynamically in the program code, the params can be serialized/deserialized and inspected via this ABI overlay. This enables dynamic calls provided by users to be supported in an elegant and simple way.

The ABI also aids in debugging since when the overlay is loaded, then calldata can be inspected. Then we can inspect txs in Python, with exported ABIs saved as JSON files per contract documenting each function's params.

Events

Custom apps will need to subscribe to blockchain txs, and be able to respond to certain events. In Ethereum, there is a custom mechanism called events. This allows smart contracts to return values to the UI. Events are indexed in the database.

An equivalent mechanism in DarkFi, may be the ability to emit events which wallets can subscribe to. As for storing them an indexed DB, we already offer that functionality with db_set() during the update phase.

The emitted event could consist of the ContractId/FunctionId, an optional list of topics, and a binary blob.

Alternatively, wallets would have to listen to all calls of a specific FunctionId. This allows wallets to only subscribe to some specific aspect of those calls.

Solana by contrast allows the RPC to subscribe to accounts directly. The equivalent in our case, is subscribing to db_set() calls. Wallets can also receive these state changes and reflect them in their UI. An EventEmitter was recently added to Solana.

Adding an explicit event emitter allows sending specific events used for wallets. This makes dev on the UI side much easier. Additionally the cost is low since any events emitted with no subscribers for that contract or not matching the filter will just be immediately dropped.

Transaction lifetime

Let $T$ be a transaction on the DarkFi network. Each transaction consists of multiple ordered contract calls:

$$T=[C_1,\dots ,C_n]$$

Associate with each contract call an operator $fC=$ contract_function. Each contract consists of arbitrary data which is interpreted by the contract. So for example sending money to a person, the transaction $T=[C_1]$ has a single call with $f{C}_1=$ Money::Transfer. To enforce a transaction fee, we can add another call to Money::Fee and now our transaction $T$ would have two calls: $[C_1,C_2]$.

To move money from a DAO's treasury, we can build a transaction $T=[C_1,C_2,C_3]$ where:

• $f{C}_1=$ Money::Fee
• $f{C}_2=$ Money::Transfer
• $f{C}_3=$ DAO::Exec

This illustrates the concept of chaining function calls together in a single transaction.

Money::Transfer

Denote the call data here simply by $C$. Since payments on DarkFi use the Sapling UTXO model, there are $n$ inputs $I_i$ and $m$ outputs $O_j$ in $C$. There are also ${\pi }_n$ input burn zero-knowledge proofs, and ${\mu }_m$ output mint zero-knowledge proofs.

Each input $I_i$ contains a nullifier $N_i$ which is deterministically generated from the previous output's (the output which is being spent) serial code ${\rho }_i$ and secret key $x_i$. The ZK burn proof ${\pi }_i$ states:

1. Correct construction of the nullifier $N_i=\text{hash}(x_i,{\rho }_i)$, revealing this value publicly.
2. Derive the public key $P_i=x_{i}G$.
3. Construct the coin commitment $C_i=\text{hash}(x_i,v_i,{\tau }_i,{\rho }_i,\dots ,b_i)$, where $v_i$ is the coin value, ${\tau }_i$ is the token ID, and $b_i$ is a random blinding factor. Additional metadata may be stored in this coin commitment for additional functionality.
4. Set membership proof that $C_i\in R$ where $R$ represents the set of all presently existing coins.
5. Any additional checks such as value and token commitments.

Outputs $O_j$ contain the public coin commitment $C_j$, a proof of their construction ${\mu }_j$, and corresponding value/token commitments. The unlinkability property comes from only the nullifier $N$ being revealed in inputs (while $C$ is hidden), while the coin $C$ appears in outputs (but without nullifiers). Since there is a deterministic derivation of nullifiers from $C$, you cannot double spend coins.

The ZK mint proof is simpler and consists of proving the correct construction of $C$ and the corresponding value/token commitments.

To hide amounts, both proofs export value commitments on the coin amounts. They use a commitment function with a homomorphic property:

$$\varphi :\mathbb{F}\to E$$ $$\varphi (x+y)=\varphi (x)+\varphi (y)$$

So to check value is preserved across inputs and outputs, it's merely sufficient to check: $$\sum _{u_i\in U}\varphi (u_i)=\sum _{v_j\in V}\varphi (v_j)$$

DAO::Exec

Earlier we mentioned that bullas/coins can contain arbitrary metadata (indicated by …). This allows us to construct the concept of protocol owned liquidity. Inside the coin we can store metadata that is checked for correctness by subsequent contract calls within the same transaction. Take for example $T=[C_1,C_2]$ mentioned earlier. We have:

• $f{C}_1=$ Money::Transfer
• $f{C}_2=$ DAO::Exec

Now the contract $C_2$ will use the encrypted DAO value exported from $C_1$ in its ZK proof when attempting to debit money from the DAO treasury. This enables secure separation of contracts and also enables composability in the anonymous smart contract context.

The DAO proof states:

1. There is a valid active proposal $P$, and $P=\text{hash}(Q,v,\dots ,D)$, where $(Q,v)$ are the destination public key and amount, and $D$ is the DAO commitment.
2. That $D=\text{hash}(q,r,\dots )$ where $q$ is the quorum threshold that must be met (minimum voting activity) and $r$ is the required approval ratio for votes to pass (e.g. 0.6).
3. Correct construction of the output coins for $C_1$ which are sending money from the DAO treasury to $(Q,v)$ are specified by the proposal, and returning the change back to the DAO's treasury.
4. Total sum of votes meet the required thresholds $q$ and $r$ as specified by the DAO.

By sending money to the DAO's treasury, you add metadata into the coin which when spent requires additional contract calls to be present in the transaction $T$. These additional calls then enforce additional restrictions on the structure and data of $T$ such as is specified above.

DAO Short Explainer

Prerequisites

There is a scheme called commit-and-reveal, where given an object $x$ (or set of objects), you generate a random blind $b$, and construct the commitment $C=\text{hash}(x,b)$. By publishing $C$, you are commmitted to the value $x$.

Secondly, we may wish to publish long lived objects on the blockchain, which are essentially commitments to several parameters that represent an object defining its behaviour. In lieu of a better term, we call these bullas.

DAO::mint(): Establishing the DAO

From darkfi/src/contract/dao/proof/dao-mint.zk:

	bulla = poseidon_hash(
		dao_proposer_limit,
		dao_quorum,
		dao_approval_ratio_quot,
		dao_approval_ratio_base,
		gov_token_id,
		dao_public_x,
		dao_public_y,
		dao_bulla_blind,
	);

Brief description of the DAO bulla params:

• proposer_limit: minimum deposit required for proposals to become valid. TODO: rename to min_deposit.
• quorum: minimum threshold of votes before it's allowed to pass. Normally this is implemented as min % of voting power, but we do this in absolute value
• approval_ratio: proportion of winners to losers for a proposal to pass.

Currently there is no notion of veto although it could be trivially added if desired.

DAO::propose(): Propose the Vote

From darkfi/src/contract/dao/proof/dao-propose-main.zk:

	proposal_bulla = poseidon_hash(
		proposal_dest_x,
		proposal_dest_y,
		proposal_amount,
		proposal_token_id,
		dao_bulla,
		proposal_blind,
	);

We create a proposal which will send tokens to the dest provided. This will soon be changed to be generic. Proposals will commit to calling params or code instead.

DAO::vote(): Vote on a Proposal

Governance token holders each make an encrypted homomorphic commitment to their vote. The homomorphism is additive so $f(u)+f(v)=f(u+v)$. They also encrypt their vote to the DAO pubkey.

Finally once voting is completed, the holders of the DAO pubkey (which is up to DAO policy) can decrypt the votes $f(v_1),\dots ,f(v_n)$, sum the values $v_1+\cdots +v_n$ and so have the value which can be used in ZK proofs alongside the publicly available commitment $f(v_1+\cdots +v_n)=f(v_1)+\cdots +f(v_n)$.

DAO::exec(): Execute Passed Proposal

This is the key part. We produce a tx which has two contract calls: [money::transfer(), DAO::exec()]. The coins spent in money::transfer() belong to the DAO and have the condition that they can only be spent when combined with DAO::exec(). Here is what coins in money::transfer() look like:

	C = poseidon_hash(
		pub_x,
		pub_y,
		value,
		token,
		serial,
		spend_hook,
		user_data,
	);

When we send coins to the DAO treasury, we set spend_hook to the DAO contract, and user_data to the DAO bulla.

When spending the coins, they reveal the spend_hook publicly and user_data (encrypted). money::transfer() enforces that the next contract call must be the same as the spend_hook.

The contract invoked by spend_hook can then use the user_data. We use this to store the DAO bulla. DAO::exec() will then use this as our DAO, and check the proposal we are executing belongs to this DAO through the reference to the DAO bulla in the proposal params.

DAO::exec() then encodes the rules that specify there has to be a valid proposal where voting passed the threshold and so on.

Assuming both contracts validate successfully, the funds are transferred out of the DAO treasury.

Formalism

Let the $C$ be the category for all sets of coins $C$ with one-way arrows $C\to C^{\prime }$ such that $C\subseteq C^{\prime }$ and an initial object $C_0=\varnothing$. We require that arrows with the same source and target commute. $$\begin{array}{ccc}C& \stackrel{c_b}{\to }& C_b\\ c_a\downarrow & & c_a^{\prime }\downarrow \\ C_a& \stackrel{c_b^{\prime }}{\to }& C_{ab}\end{array}$$

We define the nullifier functor $N:C^{\text{op}}\to N$ which is an isomorphism of $C$ that reverses arrows.

$$\begin{array}{ccc}C& \to & NC\\ c\downarrow & & \uparrow Nc\\ C^{\prime }& \to & N{C}^{\prime }\end{array}$$ We can see the action of adding $c$ to $C$ (expressed as the left downwards arrow) gets lifted to the arrow going backwards in the nullifier category. The collection of arrows in $C$ and $N$ then describes the coins and nullifier sets which are represented in merkle trees.

From the diagram we see that $C\to C^{\prime }\to N{C}^{\prime }\to NC\to C$ so that $Nc$ cancels $c$. Pasting diagrams together, we get

$$\begin{array}{ccc}{C}_0& \to & N{C}_0\\ c_1\downarrow & & \uparrow N{c}_1\\ C_1& \to & N{C}_1\\ c_2\downarrow & & \uparrow N{c}_2\\ C_2& \to & N{C}_2\end{array}$$ where all squares commute. Since all paths in $C$ are one way, proving a coin $c_k:C_{k-1}\to C_k$ exists is equivalent to being at any state $C_k,C_{k+1},C_{k+2},\dots$.

Lemma: If our state is $C_k$ then our set must contain the coins represented as arrows $c_1,\dots ,c_k$.

Anon Voting Mechanics

When making a proposal, we need to prove ownership of a threshold of coins. Likewise for voting. Essentially they are similar problems of proving ownership of a coin $c$ that is still valid. As showed above this reduces to the following statements:

• Is $c$ in the set of all coins $C$?
• If yes, then is $n(c)$ not in the set of nullifiers $N$?

Normally this logic is handled by transfers, but we need to additionally check it without leaking info about $c$. Since $n(c)$ is derived deterministically, leaking $n(c)$ also leaks info on $c$.

Nullifiers must be checked otherwise expired coins can be used.

Forking the Global State

The first method involves copying the coins state $C$. Every proof makes use of $C$ while revealing $n(c)$ which is checked against the current nullifier state. To avoid anonymity leaks from revealing $n(c)$, we additionally move the coin using a Money::transfer() call.

The downside is that wallets need to:

• Keep track of the coins tree $C$. This will involve logic to periodically checkpoint the incremental tree in a deterministic way.
• When doing any action, the wallet must move coins simultaneously. Wallets must also keep track of the unspent coin since for example it might be used in another vote (or the wallet makes a proposal and wants to vote with the same coin).

Additionally you cannot obtain a coin then vote. You must own the coin before the vote is proposed.

Forking the Global State (with SMT)

Instead of revealing the nullifier, we instead snapshot the the nullifier tree alongside $C$.

The downsides are:

• More expensive for voters since SMT is expensive in ZK.
• We're taking an older snapshot of the coins state. Spent coins spent after the vote are proposed will still be able to vote.

Tracking Coins with Local State

Each coin's user_data contains an SMT of all proposals they voted in. When transferring a coin, you must preserve this user_data. The spend_hook only allows modifying it with a parent call that adds proposals when voting to the SMT field in the coin.

The downside for wallets is that:

• The SMT committed to is large and needs to be transferred to receivers when sending the coin.
  • Alternatively coins could contain a special key (also in the user_data field), which when voting you must make a verifiable encryption. That way wallets can later scan all proposals for a DAO to find where their particular governance token voted.
• It's very complex. For example, can DAOs own governance tokens? So far DAO tokens must have the spend_hook set, but with this, we now require another spend_hook which preserves the SMT when transferring coins. The mechanics for two parents of a call aren't specified, so we'd maybe have to add some concept of symlinks.

However while complex, it is the most accurate of all 3 methods reflecting the current state.

Tree States On Disk

This section is not specific to DAO or Money, but describes a generic set abstraction which you can add or remove items from.

Requirements:

• Add and remove items, which is represented by two G-sets denoted coins $C_k$ and nullifiers $N_k$. Let $R_k$ and $S_k$ be commitments to them both respectively.
• Given any snapshot $(R_k,S_k)$, it's possible to definitively say whether the set it represents contains an item $x$ or not.
  • Be able to do this fully ZK.
• Wallets can easily take any snapshot, and using delta manipulation of the state, be able to make inclusion and exclusion proofs easily.
• Verify in WASM that $R_k$ and $S_k$ correspond to the same $k$.

The proposal is as follows and involves a merkle tree $\mathbf{C}$, and a SMT $\mathbf{N}$.

For the sake of clarity, we will not detail the storing of the trees themselves. For $\mathbf{C}$, the tree is stored in db_info, while $\mathbf{N}$ has a full on-disk representation. Instead the info in this section concerns the auxilliary data required for using the trees with snapshotted states.

DB Merkle Roots

This is used to quickly lookup a state commitment for $\mathbf{C}$ and figure out when it occurred.

We call get_tx_location(tx_hash) -> (block_height, tx_index), and then use the (block_height, tx_index) tuple to figure out all info about this state change (such as when it occurred).

DB SMT Roots

Just like for the merkle case, we want to quickly see whether $R_k$ and $S_k$ correspond to each other. We just compare the tx hash and call index. If they match, then they both exist in the same update() call.

DB Coins (Wallets)

This DB is maintained by the user wallet, and periodic garbage collection will remove values older than a cutoff.

Keeps track of values added to $\mathbf{C}$ or $\mathbf{N}$.

For $\mathbf{C}$ given an earlier tree checkpoint state, we can rewind, then fast forward to have a valid merkle tree for the given snapshot. Wallets should additionally periodically copy the merkle tree $\mathbf{C}$.

In the case of $\mathbf{N}$, we construct an overlay for SMT, which allows rewinding the tree so exclusion proofs can be constructed.

This structure for the keys in an ordered B-Tree, means it can be iterated from any point. We can start from any location from our last stored merkle tree checkpoint, and iterate forwards adding coins until we reach our desired snapshot $(R_k,S_k)$. We then have a valid merkle tree and SMT reconstructed and can create the desired inclusion or exclusion proofs.

Q: should this be 2 databases or one? If we use 2 then we can remove the type byte. Maybe more conceptually clearer?

Wallet Notes

Optimizing Note Decryption

See DAGSync: Graph-aware Zcash wallets by str4d.

TLDR: as we're syncing the wallet, we normally scan forwards prioritizing both sends and receives the same. Instead we can optimize this for immediate spendability (despite not having full received balance). Assume we have the entire blockchain state but haven't yet trial decrypted all notes.

• Nullifier Tracking: for every note, look for a nullifier. If it doesn't exist then the note has not yet been spent.
• Targeted Decryption: when the nullifier exists, then check the output notes of that transaction. One of these is likely to be change we can spend.

Additionally:

• Source Discovery: go backwards from the latest block and trial decrypt outputs. Then for those decrypted outputs, check their nullifiers (as per nullifier tracking above).
• History Discovery: simultaneously another scan goes forwards from the last sync point until it meets the source discovery (going backwards).

Knitting is where periodically wallets will gather all unspent coins and construct a new one. It will use the memo field to indicate to wallet sync that it doesn't need to go back any further than this point.

However since wallets keep track of their own coins (assuming a wallet isn't shared between 2 devices) which is the majority usecase, then this technique is less relevant since you know which coins you've spent.

Modules and Addons

The current standard model for smart contract cryptocurrencies is to abuse the web browser's plugin architecture. This has several undesirable effects:

• Dependency on js.
• Poor security model.
• Centralized frontends. The frontend can be loaded via IPFS (usually via a gateway), but it still needs to access a hosted RPC. Users can deploy their own and then configure the RPC URL but this is complicated so it rarely happens. Then there are projects for "decentralized RPC" but this is lipstick on a cow (the bloated browser).
  • Hosted frontends are a legal risk. See TornadoCash.
• Limitations of the browser addon architecture. I cannot for example run a p2p network and must go through some centralized "solution" (not a solution but actually an anti-pattern).
  • Firefox used to have a much stronger XUL framework which enabled cool things like remote CLI control of the browser or interfacing with other tools, but they deleted this and just put Chrome's addon architecture which made a whole load of addons no longer possible.
• Non-portable. Running metamask ethereum apps on mobile is generally non-trivial. Wallets should easily work across all platforms and devices seamlessly.
  • Metamask has a separate standalone Android app which is non-ideal since now the big app has 2 separate impls. Ideally there is just one big app since diverging impls lead to fragmentation.
• The architecture is specific to browsers and non-portable to other software unless they include a browser engine like WebKit which is a huge chunk of code.

Benefits of hackable software are:

• Small tools, not big apps. The software is just a minimal shell. All functionality exists as plugins.
• User extendable, which allows community control over the direction and use of the software.
  • Niche users can find a plugin for their edgecase which might not be supported in the big app.
• Easy entry for devs that have an idea compared to making a new app or tool.
  • Blender has a built in Python terminal, and the code is fully introspectable which allows exploring the codebase and calling help(foo) on objects.
• Most major successful products are hackable. Important examples: WinAmp, Blender3D, Firefox.

Addons

Addons are sandboxed WASM code which has tightly controlled permissions. They are untrusted third party 'apps'.

Most functionality are the client code for wallets. For example we want to use the DAO contract so we download an addon. An addon may provide this functionality:

• An API that can be called by other addons.
• A UI schema for building an interface.
• Transaction scanner that can do things like trial decryption of notes, maintaining any client specific state.

Addons should be sandboxed. By default access to all host functions is blacklisted, and they must be explicitly whitelisted to call any function, including other addons.

We can run addons in separate threads so that if one of them crashes, the host application can simply kill the process. Addons can then run alongside each other without any effect on each other. However this leads to increased memory usage from the overhead of having every addon spawning a new thread, so we may wish to use WASM functionality to interpret addon functions that take too long.

There is a special function inside the WASM which is called on startup called requested_permissions(). This is used to request the permissions from the user who then adds it to the whitelist for this addon. While the requested permissions will be a list of namespaced functions, the UI will simply display these as something simple to the user like "manage a database" or "use event graph" (see below).

Addons are loaded dynamically and can be downloaded from a source such as the DHT network.

Blender's addon browser looks much better than Firefox's.

When creating addon UIs, there should be a way to allow live reloading of the UI for convenient design, and possibly the impl too which makes live debugging possible.

Addon Maintenance

Overtime there will be a tension between upgrading the core API and maintaining a large ecosystem of addons. Therefore there should be a centralized git repo for all addons listed in the wallet. Addon authors can tag releases and request their addon be updated downstream by the wallet maintainers.

This way when large breaking API changes are needed, we have the ability to:

• Simultaneously update all addons at once.
• Communicate with addon authors to coordinate any changes needed such as architectural ones.
• Ensure a canonical repository of vetted addons.

This is similar to how Linux distributions maintain packages.

Addons must also have contact details so darkfi core and the wallet team are able to contact them.

Modules

These are dynamic objects which are trusted and provide full access to the host system.

An example of such a module could be an event_graph module. This enables addons to request a specific event graph instance. For example the users of a DAO may wish to coordinate through the p2p network. They would therefore use the event_graph module to create an event graph instance for that usecase, and the p2p network would create a swarm for this event graph. All of this would be handled by the module which simply provides a convenient interface to the addon.

This enables using the full power of the system, but safely segregating this functionality from untrusted addons through a firewall. It solves the issue of relying on hosted/centralized gateways since user wallets will just spin up p2p nodes locally.

Modules can only be installed manually from file and require restarting the wallet.

Scenegraph

This is a popular gamedev design pattern where the entire program state is represented as an introspectable tree. It's similar to the UNIX pattern of "everything is a file", and maybe plan9's idea.

The scenegraph is a world where the children are objects, and the objects have attributes that can be read and operated on. These can all be composed together through generic node interfaces.

example of a scenegraph from a game engine

scenegraph in blender

Application
    SettingsRegistry
    Window #1
        TabBar
            Tab #1
                Panel #1
                    WasmSandbox
                        ...
                Panel #2
                ...
            Tab #2
                ...
            ...
    Window #2
        ...
    Module #1

• Each object can emit events, and subscribe to events from other objects. All objects have an event() method and update() method. Update is called per frame, while event can be used for timer events such as periodic updates or wakeups, as well as input events.
• Drawing related objects have a boundary where they can draw. They all implement a draw() method. Drawing outside the boundary is disallowed.
• Everything has names, attributes and methods with docstrings. This is all introspectable and eventually scriptable. Also the internal state can be accessed through inbuilt terminal, possibly using Python.

UI Specifics

Laundry list of required features:

• XUL/bpy inspired. There is a small wallet core, but the entire UI is created using definitions and the DSL.
• Dynamic fractional scaling.
• Customizable scriptable interface, preferably using Python and/or Rust.
• Calm UI with default darkmode. No animations.
• Text oriented, clean and minimal design.
• Avoid modal dialogs. Instead use mode toggling and expanding panels.
  • The UI should enable you to view all relevant options and tools at a glance, without the need for pushing or dragging windows around.
  • Tools and interface options designed to not block the user from using any other parts.
    • The UI should stay responsive by all means.
      • This means the UI runs in its own thread, communicating with the backend which runs on another thread.
      • Non blocking and async. Remains responsive despite work happening.
  • User input should remain as consistent and predictable as possible.
• Installation free: run out of the box for new installs, not requiring root system access.
• Responsive design across desktop and mobile devices with minimal specific code or changes required. Ideally none at all.
• First class CLI support with access to all functionality existing in the UI.
  • Possibly there is a way of transforming the UI schema specced by addons into a command line interface.

See also the Blender Human Interface Guidelines: Paradigms.

Roadmap

1. Simple drk CLI tool with basic core apps working. We want to ship so this is the only core prerequisite to start.
2. We can add WASM addons with the basic framework after. Then migrate core apps such as money or DAO to this.
3. Add modules subsystem.
4. Construct the UI.
5. Create the overall framework of resizable 'editors' and define the terminology.
6. Add in the scripting functionality for the UI.
7. Ensure cross-platform support and clean architecture.
8. Iterate on finer UI design specifics.
9. Allow customization of UI such as colors and style (optional).

Steps 3 and 4 can be done in parallel.

References

• Veil: Private Browsing Semantics Without Browser-side Assistance
• Atlantis: Robust, Extensible Execution Environments for Web Applications

zkas

zkas is a compiler for the Halo2 zkVM language used in DarkFi.

The current implementation found in the DarkFi repository inside src/zkas is the reference compiler and language implementation. It is a toolchain consisting of a lexer, parser, static and semantic analyzers, and a binary code compiler.

The main.rs file shows how this toolchain is put together to produce binary code from source code.

Architecture

The main part of the compilation happens inside the parser. New opcodes can be added by extending opcode.rs.

    // The lexer goes over the input file and separates its content into
    // tokens that get fed into a parser.
    let lexer = Lexer::new(filename, source.chars());
    let tokens = match lexer.lex() {
        Ok(v) => v,
        Err(_) => return ExitCode::FAILURE,
    };

    // The parser goes over the tokens provided by the lexer and builds
    // the initial AST, not caring much about the semantics, just enforcing
    // syntax and general structure.
    let parser = Parser::new(filename, source.chars(), tokens);
    let (namespace, k, constants, witnesses, statements) = match parser.parse() {
        Ok(v) => v,
        Err(_) => return ExitCode::FAILURE,
    };

    // The analyzer goes through the initial AST provided by the parser and
    // converts return and variable types to their correct forms, and also
    // checks that the semantics of the ZK script are correct.
    let mut analyzer = Analyzer::new(filename, source.chars(), constants, witnesses, statements);
    if analyzer.analyze_types().is_err() {
        return ExitCode::FAILURE
    }

    if iflag && analyzer.analyze_semantic().is_err() {
        return ExitCode::FAILURE
    }

    if pflag {
        println!("{:#?}", analyzer.constants);
        println!("{:#?}", analyzer.witnesses);
        println!("{:#?}", analyzer.statements);
        println!("{:#?}", analyzer.heap);
        return ExitCode::SUCCESS
    }

    let compiler = Compiler::new(
        filename,
        source.chars(),
        namespace,
        k,
        analyzer.constants,
        analyzer.witnesses,
        analyzer.statements,
        analyzer.literals,
        !sflag,
    );

    let bincode = match compiler.compile() {
        Ok(v) => v,
        Err(_) => return ExitCode::FAILURE,
    };

Writing ZK Proofs

ZK proofs in DarkFi are written in a simple low level DSL. The zkas compiler then converts this human readable code into bytecode that is run on the DarkFi ZKVM.

Zkas Usage

To build zkas, run:

make zkas

We can then see the help output with zkas -h.

To compile a .zk file, simply run:

$ zkas proof/opcodes.zk
Wrote output to proof/opcodes.zk.bin

It's worth running zkas -i proof/opcodes.zk to get a sense of what instructions the bytecode will send to the VM. We can also see the data structure with -e as well.

Structure of a ZK File

Take a look at existing ZK files in proof/ directory for examples. See also src/contract/dao/proof/ and src/contract/money/proof/. In all of those directories is a witness/ subdirectory containing witness JSON files that can be used with the zkrunner and zkrender tools below.

k = ... indicates the number of rows which is $2^k$. Bigger values make your proof slower, whereas if k is too low then the proof generation will fail. Pick a value that works and find the minimum allowed. Usually 11 to 13 works.

field = "pallas" indicates the base field.

The constant section specifies any constants we use.

witness section contains the witnesses provided when generating the proof.

circuit specifies the actual instructions for the proof.

Generating a ZK Proof in Rust

When compiling you will need to use the zk feature in cargo. Check tests/zkvm_opcodes.rs for an example to follow along with.

The broad steps are:

1. Create your witness values, and put them in an array. The order must match what is set in the .zk file.
2. Calculate the public values from the private witnesses. This must be an array of the same type (usually pallas::Base).
3. Load the bytecode and generate the ZK proof.
4. Optionally you can verify it.

Debugging ZK Files

The first thing you should do is export a JSON file to run with the debugger. You can do this by adding this line into Rust.

zk::export_witness_json("witness.json", &prover_witnesses, &public_inputs);

Then after running the code, you should now have a file called witness.json.

Then run the ZK debugger.

./bin/zkrunner/zkrunner.py -w witness.json --prove --trace foo.zk

where foo.zk is our .zk file we're debugging.

Often this works, but the ZK proof is failing when used with a WASM contract. In that case the culprit is that the WASM code is exporting the wrong public values. Use the msg!() macro to print them to the program's output log, and compare it with the public values you see in the witness.json from when the proof was created. This will allow you to pinpoint exactly where the error occurs.

For example files to try, see the comment in the section above Structure of a ZK File.

Viewing the ZK Circuit Layout

ZK circuit have a layout. The less empty space, the more efficient is your circuit. Usually it just means reducing the k value specified. The number of rows in your circuit is $2^k$, so reducing the value by 1 will halve the number of rows.

To generate an image of the circuit layout, simply run:

./bin/zkrunner/zkrender.py -w src/contract/dao/proof/witness/exec.json src/contract/dao/proof/exec.zk /tmp/layout.png

You should see something like:

zkas bincode

The bincode design for zkas is the compiled code in the form of a binary blob, that can be read by a program and fed into the VM.

Our programs consist of four sections: constant, literal, witness, and circuit. Our bincode represents the same. Additionally, there is an optional section called .debug which can hold debug info related to the binary.

We currently keep all variables on one heap, and literals on another heap. Therefore before each HEAP_INDEX we prepend HEAP_TYPE so the VM is able to know which heap it should do lookup from.

The compiled binary blob has the following layout:

MAGIC_BYTES
BINARY_VERSION
K
NAMESPACE
.constant
CONSTANT_TYPE CONSTANT_NAME 
CONSTANT_TYPE CONSTANT_NAME 
...
.literal
LITERAL
LITERAL
...
.witness
WITNESS_TYPE
WITNESS_TYPE
...
.circuit
OPCODE ARG_NUM HEAP_TYPE HEAP_INDEX ... HEAP_TYPE HEAP_INDEX
OPCODE ARG_NUM HEAP_TYPE HEAP_INDEX ... HEAP_TYPE HEAP_INDEX
...
.debug
TBD

Integers in the binary are encoded using variable-integer encoding. See the serial crate and module for our Rust implementation.

Sections

MAGIC_BYTES

The magic bytes are the file signature consisting of four bytes used to identify the zkas binary code. They consist of:

0x0b 0x01 0xb1 0x35

BINARY_VERSION

The binary code also contains the binary version to allow parsing potential different formats in the future.

0x02

K

This is a 32bit unsigned integer that represents the k parameter needed to know how many rows our circuit needs.

NAMESPACE

This sector after MAGIC_BYTES, BINARY_VERSION, and K contains the reference namespace of the code. This is the namespace used in the source code, e.g.:

constant "MyNamespace" { ... }
witness  "MyNamespace" { ... }
circuit  "MyNamespace" { ... }

The string is serialized with variable-integer encoding.

.constant

The constants in the .constant section are declared with their type and name, so that the VM knows how to search for the builtin constant and add it to the heap.

.literal

The literals in the .literal section are currently unsigned integers that get parsed into a u64 type inside the VM. In the future this could be extended with signed integers, and strings.

.witness

The .witness section holds the circuit witness values in the form of WITNESS_TYPE. Their heap index is incremented for each witness as they're kept in order like in the source file. The witnesses that are of the same type as the circuit itself (typically Base) will be loaded into the circuit as private values using the Halo2 load_private API.

.circuit

The .circuit section holds the procedural logic of the ZK proof. In here we have statements with opcodes that are executed as understood by the VM. The statements are in the form of:

OPCODE ARG_NUM HEAP_TYPE HEAP_INDEX ... HEAP_TYPE HEAP_INDEX

where:

In case an opcode has a return value, the value shall be pushed to the heap and become available for later references.

.debug

TBD

Syntax Reference

Variable Types

Literal Types

Opcodes

Built-in Opcode Wrappers

Decoding the bincode

An example decoder implementation can be found in zkas' decoder.rs module.

zkVM

The DarkFi zkVM is a single zkSNARK circuit based on Halo2 which requires no trusted setup and is able to execute and prove compiled zkas bincode.

The zkVM is designed in such a way that it's able to choose code paths based on the bincode and as such, create a zkSNARK proof specific to the zkas circuit. In this document, we'll explain this machinery from a high level. A preliminary to understanding the zkVM is to understand the zkas bincode and its layout.

High-level operation

The entire VM can be thought of as a machine with heap access to values (variables) that are constructed within the ZK circuit. Upon initialization, the VM instantiates two heaps, of which one holds literals (currently u64 is supported), and the other holds arbitrary types defined in HeapVar

Once the heaps are instantiated, the circuit initializes all the available halo2 gadgets so they're ready for use, and also to create and have access to any lookup tables.

Next, if there are any constants defined in the constant section of zkas, they are created and pushed to the heap:

        // Lookup and push constants onto the heap
        for constant in &self.constants {
            trace!(
                target: "zk::vm",
                "Pushing constant `{}` to heap address {}",
                constant.as_str(),
                heap.len()
            );
            match constant.as_str() {
                "VALUE_COMMIT_VALUE" => {
                    let vcv = ValueCommitV;
                    let vcv = FixedPointShort::from_inner(ecc_chip.as_ref().unwrap().clone(), vcv);
                    heap.push(HeapVar::EcFixedPointShort(vcv));
                }
                "VALUE_COMMIT_RANDOM" => {
                    let vcr = OrchardFixedBasesFull::ValueCommitR;
                    let vcr = FixedPoint::from_inner(ecc_chip.as_ref().unwrap().clone(), vcr);
                    heap.push(HeapVar::EcFixedPoint(vcr));
                }
                "VALUE_COMMIT_RANDOM_BASE" => {
                    let vcr = ConstBaseFieldElement::value_commit_r();
                    let vcr =
                        FixedPointBaseField::from_inner(ecc_chip.as_ref().unwrap().clone(), vcr);
                    heap.push(HeapVar::EcFixedPointBase(vcr));
                }
                "NULLIFIER_K" => {
                    let nfk = ConstBaseFieldElement::nullifier_k();
                    let nfk =
                        FixedPointBaseField::from_inner(ecc_chip.as_ref().unwrap().clone(), nfk);
                    heap.push(HeapVar::EcFixedPointBase(nfk));
                }

                _ => {
                    error!(target: "zk::vm", "Invalid constant name: {}", constant.as_str());
                    return Err(plonk::Error::Synthesis)
                }
            }
        }

If all is successful, the VM proceeds with any available literals in the circuit section and pushes them onto the literals heap:

        // Load the literals onto the literal heap
        // N.B. Only uint64 is supported right now.
        for literal in &self.literals {
            match literal.0 {
                LitType::Uint64 => match literal.1.parse::<u64>() {
                    Ok(v) => litheap.push(v),
                    Err(e) => {
                        error!(target: "zk::vm", "Failed converting u64 literal: {}", e);
                        return Err(plonk::Error::Synthesis)
                    }
                },
                _ => {
                    error!(target: "zk::vm", "Invalid literal: {:?}", literal);
                    return Err(plonk::Error::Synthesis)
                }
            }
        }

At this point, the VM is done with initializing the constants used, and proceeds with the private witnesses of the ZK proof that are located in the witness section of the zkas bincode. We simply loop through the witnesses in order, and depending on what they are, we witness them with specialized halo2 functions:

        // Push the witnesses onto the heap, and potentially, if the witness
        // is in the Base field (like the entire circuit is), load it into a
        // table cell.
        for witness in &self.witnesses {
            match witness {
                Witness::EcPoint(w) => {
                    trace!(target: "zk::vm", "Witnessing EcPoint into circuit");
                    let point = Point::new(
                        ecc_chip.as_ref().unwrap().clone(),
                        layouter.namespace(|| "Witness EcPoint"),
                        w.as_ref().map(|cm| cm.to_affine()),
                    )?;

                    trace!(target: "zk::vm", "Pushing EcPoint to heap address {}", heap.len());
                    heap.push(HeapVar::EcPoint(point));
                }

                Witness::EcNiPoint(w) => {
                    trace!(target: "zk::vm", "Witnessing EcNiPoint into circuit");
                    let point = NonIdentityPoint::new(
                        ecc_chip.as_ref().unwrap().clone(),
                        layouter.namespace(|| "Witness EcNiPoint"),
                        w.as_ref().map(|cm| cm.to_affine()),
                    )?;

                    trace!(target: "zk::vm", "Pushing EcNiPoint to heap address {}", heap.len());
                    heap.push(HeapVar::EcNiPoint(point));
                }

                Witness::EcFixedPoint(_) => {
                    error!(target: "zk::vm", "Unable to witness EcFixedPoint, this is unimplemented.");
                    return Err(plonk::Error::Synthesis)
                }

                Witness::Base(w) => {
                    trace!(target: "zk::vm", "Witnessing Base into circuit");
                    let base = assign_free_advice(
                        layouter.namespace(|| "Witness Base"),
                        config.witness,
                        *w,
                    )?;

                    trace!(target: "zk::vm", "Pushing Base to heap address {}", heap.len());
                    heap.push(HeapVar::Base(base));
                }

                Witness::Scalar(w) => {
                    trace!(target: "zk::vm", "Witnessing Scalar into circuit");
                    let scalar = ScalarFixed::new(
                        ecc_chip.as_ref().unwrap().clone(),
                        layouter.namespace(|| "Witness ScalarFixed"),
                        *w,
                    )?;

                    trace!(target: "zk::vm", "Pushing Scalar to heap address {}", heap.len());
                    heap.push(HeapVar::Scalar(scalar));
                }

                Witness::MerklePath(w) => {
                    trace!(target: "zk::vm", "Witnessing MerklePath into circuit");
                    let path: Value<[pallas::Base; MERKLE_DEPTH_ORCHARD]> =
                        w.map(|typed_path| gen_const_array(|i| typed_path[i].inner()));

                    trace!(target: "zk::vm", "Pushing MerklePath to heap address {}", heap.len());
                    heap.push(HeapVar::MerklePath(path));
                }

                Witness::SparseMerklePath(w) => {
                    let path: Value<[pallas::Base; SMT_FP_DEPTH]> =
                        w.map(|typed_path| gen_const_array(|i| typed_path[i]));

                    trace!(target: "zk::vm", "Pushing SparseMerklePath to heap address {}", heap.len());
                    heap.push(HeapVar::SparseMerklePath(path));
                }

                Witness::Uint32(w) => {
                    trace!(target: "zk::vm", "Pushing Uint32 to heap address {}", heap.len());
                    heap.push(HeapVar::Uint32(*w));
                }

                Witness::Uint64(w) => {
                    trace!(target: "zk::vm", "Pushing Uint64 to heap address {}", heap.len());
                    heap.push(HeapVar::Uint64(*w));
                }
            }
        }

Once this is done, everything is set up and the VM proceeds with executing the input opcodes that are located in the circuit section of the zkas bincode in a sequential fashion. Opcodes are able to take a defined number of inputs and are able to optionally produce a single output. The inputs are referenced from the heap, by index. The output that can be produced by an opcode is also pushed onto the heap when created. An example of this operation can be seen within the following snippet from the zkVM:

        for opcode in &self.opcodes {
            match opcode.0 {
                Opcode::EcAdd => {
                    trace!(target: "zk::vm", "Executing `EcAdd{:?}` opcode", opcode.1);
                    let args = &opcode.1;

                    let lhs: Point<pallas::Affine, EccChip<OrchardFixedBases>> =
                        heap[args[0].1].clone().try_into()?;

                    let rhs: Point<pallas::Affine, EccChip<OrchardFixedBases>> =
                        heap[args[1].1].clone().try_into()?;

                    let ret = lhs.add(layouter.namespace(|| "EcAdd()"), &rhs)?;

                    trace!(target: "zk::vm", "Pushing result to heap address {}", heap.len());
                    self.tracer.push_ecpoint(&ret);
                    heap.push(HeapVar::EcPoint(ret));
                }

As the opcodes are being executed, the halo2 API lets us return any possible proof verification error so the verifier is able to know if the input proof is valid or not. Any possible public inputs to a circuit are also fed into the constrain_instance opcode, so that's how even public inputs can be enforced in the same uniform fashion like the rest.

Examples

This section holds practical and real-world examples of the use for zkas.

• Sapling payment scheme
• Anonymous voting

Anonymous voting

Anonymous voting¹ is a type of voting process where users can vote without revealing their identity, by proving they are accepted as valid voters.

The proof enables user privacy and allows for fully anonymous voting.

The starting point is a Merkle proof², which efficiently proves that a voter's key belongs to a Merkle tree. However, using this proof alone would allow the organizer of a process to correlate each vote envelope with its voter's key on the database, so votes wouldn't be secret.

Vote proof

k = 13;
field = "pallas";

constant "Vote" {
	EcFixedPointShort VALUE_COMMIT_VALUE,
	EcFixedPoint VALUE_COMMIT_RANDOM,
	EcFixedPointBase NULLIFIER_K,
}

witness "Vote" {
	Base process_id_0,
	Base process_id_1,
	Base secret_key,
	Base vote,
	Scalar vote_blind,
	Uint32 leaf_pos,
	MerklePath path,
}

circuit "Vote" {
	# Nullifier hash
	process_id = poseidon_hash(process_id_0, process_id_1);
	nullifier = poseidon_hash(secret_key, process_id);
	constrain_instance(nullifier);

	# Public key derivation and hashing
	public_key = ec_mul_base(secret_key, NULLIFIER_K);
	public_x = ec_get_x(public_key);
	public_y = ec_get_y(public_key);
	pk_hash = poseidon_hash(public_x, public_y);

	# Merkle root
	root = merkle_root(leaf_pos, path, pk_hash);
	constrain_instance(root);

	# Pedersen commitment for vote
	vcv = ec_mul_short(vote, VALUE_COMMIT_VALUE);
	vcr = ec_mul(vote_blind, VALUE_COMMIT_RANDOM);
	vote_commit = ec_add(vcv, vcr);
	# Since vote_commit is a curve point, we fetch its coordinates
	# and constrain_them:
	vote_commit_x = ec_get_x(vote_commit);
	vote_commit_y = ec_get_y(vote_commit);
	constrain_instance(vote_commit_x);
	constrain_instance(vote_commit_y);
}

Our proof consists of four main operation. First we are hashing the nullifier using our secret key and the hashed process ID. Next, we derive our public key and hash it. Following, we take this hash and create a Merkle proof that it is indeed contained in the given Merkle tree. And finally, we create a Pedersen commitment³ for the vote choice itself.

Our vector of public inputs can look like this:

let public_inputs = vec![
    nullifier,
    merkle_root,
    *vote_coords.x(),
    *vote_coords.y(),
]

And then the Verifier uses these public inputs to verify the given zero-knowledge proof.

Sapling payment scheme

Sapling is a type of transaction which hides both the sender and receiver data, as well as the amount transacted. This means it allows a fully private transaction between two addresses.

Generally, the Sapling payment scheme consists of two ZK proofs - mint and burn. We use the mint proof to create a new coin $C$, and we use the burn proof to spend a previously minted coin.

Mint proof

k = 13;
field = "pallas";

constant "Mint" {
	EcFixedPointShort VALUE_COMMIT_VALUE,
	EcFixedPoint VALUE_COMMIT_RANDOM,
	EcFixedPointBase NULLIFIER_K,
}

witness "Mint" {
	Base pub_x,
	Base pub_y,
	Base value,
	Base token,
	Base serial,
	Scalar value_blind,
	Scalar token_blind,
}

circuit "Mint" {
	# Poseidon hash of the coin
	C = poseidon_hash(pub_x, pub_y, value, token, serial);
	constrain_instance(C);

	# Pedersen commitment for coin's value
	vcv = ec_mul_short(value, VALUE_COMMIT_VALUE);
	vcr = ec_mul(value_blind, VALUE_COMMIT_RANDOM);
	value_commit = ec_add(vcv, vcr);
	# Since the value commit is a curve point, we fetch its coordinates
	# and constrain them:
	value_commit_x = ec_get_x(value_commit);
	value_commit_y = ec_get_y(value_commit);
	constrain_instance(value_commit_x);
	constrain_instance(value_commit_y);

	# Pedersen commitment for coin's token ID
	tcv = ec_mul_base(token, NULLIFIER_K);
	tcr = ec_mul(token_blind, VALUE_COMMIT_RANDOM);
	token_commit = ec_add(tcv, tcr);
	# Since token_commit is also a curve point, we'll do the same
	# coordinate dance:
	token_commit_x = ec_get_x(token_commit);
	token_commit_y = ec_get_y(token_commit);
	constrain_instance(token_commit_x);
	constrain_instance(token_commit_y);

	# At this point we've enforced all of our public inputs.
}

As you can see, the Mint proof basically consists of three operations. First one is hashing the coin $C$, and after that, we create Pedersen commitments¹ for both the coin's value and the coin's token ID. On top of the zkas code, we've declared two constant values that we are going to use for multiplication in the commitments.

The constrain_instance call can take any of our assigned variables and enforce a public input. Public inputs are an array (or vector) of revealed values used by verifiers to verify a zero knowledge proof. In the above case of the Mint proof, since we have five calls to constrain_instance, we would also have an array of five elements that represent these public inputs. The array's order must match the order of the constrain_instance calls since they will be constrained by their index in the array (which is incremented for every call).

In other words, the vector of public inputs could look like this:

let public_inputs = vec![
    coin,
    *value_coords.x(),
    *value_coords.y(),
    *token_coords.x(),
    *token_coords.y(),
];

And then the Verifier uses these public inputs to verify a given zero knowledge proof.

Coin

During the Mint phase we create a new coin $C$, which is bound to the public key $P$. The coin $C$ is publicly revealed on the blockchain and added to the Merkle tree.

Let $v$ be the coin's value, $t$ be the token ID, $\rho$ be the unique serial number for the coin, and $r_C$ be a random blinding value. We create a commitment (hash) of these elements and produce the coin $C$ in zero-knowledge:

$$C=H(P,v,t,\rho ,r_C)$$

An interesting thing to keep in mind is that this commitment is extensible, so one could fit an arbitrary amount of different attributes inside it.

Value and token commitments

To have some value $v$ for our coin, we ensure it's greater than zero, and then we can create a Pedersen commitment $V$ where $r_V$ is the blinding factor for the commitment, and $G_1$ and $G_2$ are two predefined generators:

$$v>0$$ $$V=v{G}_1+r_V{G}_2$$

The token ID can be thought of as an attribute we append to our coin so we can have a differentiation of assets we are working with. In practice, this allows us to work with different tokens, using the same zero-knowledge proof circuit. For this token ID, we can also build a Pedersen commitment $T$ where $t$ is the token ID, $r_T$ is the blinding factor, and $G_1$ and $G_2$ are predefined generators:

$$T=t{G}_1+r_T{G}_2$$

Pseudo-code

Knowing this we can extend our pseudo-code and build the before-mentioned public inputs for the circuit:

let bincode = include_bytes!("../proof/mint.zk.bin");
let zkbin = ZkBinary::decode(bincode)?;

// ======
// Prover
// ======

// Witness values
let value = 42;
let token_id = pallas::Base::random(&mut OsRng);
let value_blind = pallas::Scalar::random(&mut OsRng);
let token_blind = pallas::Scalar::random(&mut OsRng);
let serial = pallas::Base::random(&mut OsRng);
let public_key = PublicKey::from_secret(SecretKey::random(&mut OsRng));
let (pub_x, pub_y) = public_key.xy();

let prover_witnesses = vec![
    Witness::Base(Value::known(pub_x)),
    Witness::Base(Value::known(pub_y)),
    Witness::Base(Value::known(pallas::Base::from(value))),
    Witness::Base(Value::known(token_id)),
    Witness::Base(Value::known(serial)),
    Witness::Scalar(Value::known(value_blind)),
    Witness::Scalar(Value::known(token_blind)),
];

// Create the public inputs
let msgs = [pub_x, pub_y, pallas::Base::from(value), token_id, serial];
let coin = poseidon_hash(msgs);

let value_commit = pedersen_commitment_u64(value, value_blind);
let value_coords = value_commit.to_affine().coordinates().unwrap();

let token_commit = pedersen_commitment_base(token_id, token_blind);
let token_coords = token_commit.to_affine().coordinates().unwrap();

let public_inputs = vec![
    coin,
    *value_coords.x(),
    *value_coords.y(),
    *token_coords.x(),
    *token_coords.y(),
];

// Create the circuit
let circuit = ZkCircuit::new(prover_witnesses, zkbin.clone());

let proving_key = ProvingKey::build(13, &circuit);
let proof = Proof::create(&proving_key, &[circuit], &public_inputs, &mut OsRng)?;

// ========
// Verifier
// ========

// Construct empty witnesses
let verifier_witnesses = empty_witnesses(&zkbin);

// Create the circuit
let circuit = ZkCircuit::new(verifier_witnesses, zkbin);

let verifying_key = VerifyingKey::build(13, &circuit);
proof.verify(&verifying_key, &public_inputs)?;

Burn

k = 13;
field = "pallas";

constant "Burn" {
	EcFixedPointShort VALUE_COMMIT_VALUE,
	EcFixedPoint VALUE_COMMIT_RANDOM,
	EcFixedPointBase NULLIFIER_K,
}

witness "Burn" {
	Base secret,
	Base serial,
	Base value,
	Base token,
	Scalar value_blind,
	Scalar token_blind,
	Uint32 leaf_pos,
	MerklePath path,
	Base signature_secret,
}

circuit "Burn" {
	# Poseidon hash of the nullifier
	nullifier = poseidon_hash(secret, serial);
	constrain_instance(nullifier);

	# Pedersen commitment for coin's value
	vcv = ec_mul_short(value, VALUE_COMMIT_VALUE);
	vcr = ec_mul(value_blind, VALUE_COMMIT_RANDOM);
	value_commit = ec_add(vcv, vcr);
	# Since value_commit is a curve point, we fetch its coordinates
	# and constrain them:
	value_commit_x = ec_get_x(value_commit);
	value_commit_y = ec_get_y(value_commit);
	constrain_instance(value_commit_x);
	constrain_instance(value_commit_y);

	# Pedersen commitment for coin's token ID
	tcv = ec_mul_base(token, NULLIFIER_K);
	tcr = ec_mul(token_blind, VALUE_COMMIT_RANDOM);
	token_commit = ec_add(tcv, tcr);
	# Since token_commit is also a curve point, we'll do the same
	# coordinate dance:
	token_commit_x = ec_get_x(token_commit);
	token_commit_y = ec_get_y(token_commit);
	constrain_instance(token_commit_x);
	constrain_instance(token_commit_y);

	# Coin hash
	pub = ec_mul_base(secret, NULLIFIER_K);
	pub_x = ec_get_x(pub);
	pub_y = ec_get_y(pub);
	C = poseidon_hash(pub_x, pub_y, value, token, serial);

	# Merkle root
	root = merkle_root(leaf_pos, path, C);
	constrain_instance(root);

	# Finally, we derive a public key for the signature and
	# constrain its coordinates:
	signature_public = ec_mul_base(signature_secret, NULLIFIER_K);
	signature_x = ec_get_x(signature_public);
	signature_y = ec_get_y(signature_public);
	constrain_instance(signature_x);
	constrain_instance(signature_y);

	# At this point we've enforced all of our public inputs.
}

The Burn proof consists of operations similar to the Mint proof, with the addition of a Merkle root² calculation. In the same manner, we are doing a Poseidon hash instance, we're building Pedersen commitments for the value and token ID, and finally we're doing a public key derivation.

In this case, our vector of public inputs could look like:

let public_inputs = vec![
    nullifier,
    *value_coords.x(),
    *value_coords.y(),
    *token_coords.x(),
    *token_coords.y(),
    merkle_root,
    *sig_coords.x(),
    *sig_coords.y(),
];

Nullifier

When we spend the coin, we must ensure that the value of the coin cannot be double spent. We call this the Burn phase. The process relies on a nullifier $N$, which we create using the secret key $x$ for the public key $P$ and a unique random serial $\rho$. Nullifiers are unique per coin and prevent double spending:

$$N=H(x,\rho )$$

Merkle root

We check that the merkle root corresponds to a coin which is in the Merkle tree $R$

$$C=H(P,v,t,\rho ,r_C)$$ $$C\in R$$

Value and token commitments

Just like we calculated these for the Mint proof, we do the same here:

$$v>0$$ $$V=v{G}_1+r_V{G}_2$$ $$T=t{G}_1+r_T{G}_2$$

Public key derivation

We check that the secret key $x$ corresponds to a public key $P$. Usually, we do public key derivation my multiplying our secret key with a genera tor $G$, which results in a public key:

$$P=xG$$

Pseudo-code

Knowing this we can extend our pseudo-code and build the before-mentioned public inputs for the circuit:

let bincode = include_bytes!("../proof/burn.zk.bin");
let zkbin = ZkBinary::decode(bincode)?;

// ======
// Prover
// ======

// Witness values
let value = 42;
let token_id = pallas::Base::random(&mut OsRng);
let value_blind = pallas::Scalar::random(&mut OsRng);
let token_blind = pallas::Scalar::random(&mut OsRng);
let serial = pallas::Base::random(&mut OsRng);
let secret = SecretKey::random(&mut OsRng);
let sig_secret = SecretKey::random(&mut OsRng);

// Build the coin
let coin2 = {
    let (pub_x, pub_y) = PublicKey::from_secret(secret).xy();
    let messages = [pub_x, pub_y, pallas::Base::from(value), token_id, serial];
    poseidon_hash(messages)
};

// Fill the merkle tree with some random coins that we want to witness,
// and also add the above coin.
let mut tree = BridgeTree::<MerkleNode, 32>::new(100);
let coin0 = pallas::Base::random(&mut OsRng);
let coin1 = pallas::Base::random(&mut OsRng);
let coin3 = pallas::Base::random(&mut OsRng);

tree.append(&MerkleNode::from(coin0));
tree.witness();
tree.append(&MerkleNode::from(coin1));
tree.append(&MerkleNode::from(coin2));
let leaf_pos = tree.witness().unwrap();
tree.append(&MerkleNode::from(coin3));
tree.witness();

let root = tree.root(0).unwrap();
let merkle_path = tree.authentication_path(leaf_pos, &root).unwrap();
let leaf_pos: u64 = leaf_pos.into();

let prover_witnesses = vec![
    Witness::Base(Value::known(secret.inner())),
    Witness::Base(Value::known(serial)),
    Witness::Base(Value::known(pallas::Base::from(value))),
    Witness::Base(Value::known(token_id)),
    Witness::Scalar(Value::known(value_blind)),
    Witness::Scalar(Value::known(token_blind)),
    Witness::Uint32(Value::known(leaf_pos.try_into().unwrap())),
    Witness::MerklePath(Value::known(merkle_path.try_into().unwrap())),
    Witness::Base(Value::known(sig_secret.inner())),
];

// Create the public inputs
let nullifier = Nullifier::from(poseidon_hash::<2>([secret.inner(), serial]));

let value_commit = pedersen_commitment_u64(value, value_blind);
let value_coords = value_commit.to_affine().coordinates().unwrap();

let token_commit = pedersen_commitment_base(token_id, token_blind);
let token_coords = token_commit.to_affine().coordinates().unwrap();

let sig_pubkey = PublicKey::from_secret(sig_secret);
let (sig_x, sig_y) = sig_pubkey.xy();

let merkle_root = tree.root(0).unwrap();

let public_inputs = vec![
    nullifier.inner(),
    *value_coords.x(),
    *value_coords.y(),
    *token_coords.x(),
    *token_coords.y(),
    merkle_root.inner(),
    sig_x,
    sig_y,
];

// Create the circuit
let circuit = ZkCircuit::new(prover_witnesses, zkbin.clone());

let proving_key = ProvingKey::build(13, &circuit);
let proof = Proof::create(&proving_key, &[circuit], &public_inputs, &mut OsRng)?;

// ========
// Verifier
// ========

// Construct empty witnesses
let verifier_witnesses = empty_witnesses(&zkbin);

// Create the circuit
let circuit = ZkCircuit::new(verifier_witnesses, zkbin);

let verifying_key = VerifyingKey::build(13, &circuit);
proof.verify(&verifying_key, &public_inputs)?;

Clients

This section gives information on DarkFi's clients, such as darkfid and cashierd. Currently this section offers documentation on the client's RPC API.

darkfid JSON-RPC API

• clock
• dnet_switch
• ping_miner

clock

Returns current system clock as u64 (String) timestamp.
^[src]

--> {"jsonrpc": "2.0", "method": "clock", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "result": "1234", "id": 1}

dnet_switch

Activate or deactivate dnet in the P2P stack. By sending true, dnet will be activated, and by sending false dnet will be deactivated. Returns true on success.
^[src]

--> {"jsonrpc": "2.0", "method": "dnet_switch", "params": [true], "id": 42}
<-- {"jsonrpc": "2.0", "result": true, "id": 42}

ping_miner

Pings configured miner daemon for liveness. Returns true on success.
^[src]

--> {"jsonrpc": "2.0", "method": "ping_miner", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "result": "true", "id": 1}

blockchain methods

• blockchain.get_block
• blockchain.get_tx
• blockchain.last_known_block
• blockchain.subscribe_blocks
• blockchain.subscribe_txs
• blockchain.subscribe_proposals
• blockchain.lookup_zkas
• merge_mining_get_chain_id

blockchain.get_block

Queries the blockchain database for a block in the given height. Returns a readable block upon success.

Params:

• array[0]: u64 Block height (as string)

Returns:

• BlockInfo struct serialized into base64.
  ^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.get_block", "params": ["0"], "id": 1}
<-- {"jsonrpc": "2.0", "result": {...}, "id": 1}

blockchain.get_tx

Queries the blockchain database for a given transaction. Returns a serialized Transaction object.

Params:

• array[0]: Hex-encoded transaction hash string

Returns:

• Serialized Transaction object encoded with base64
  ^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.get_tx", "params": ["TxHash"], "id": 1}
<-- {"jsonrpc": "2.0", "result": "ABCD...", "id": 1}

blockchain.last_known_block

Queries the blockchain database to find the last known block

Params:

• None

Returns:

• u64 Height of the last known block, as string
  ^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.last_known_block", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "result": "1234", "id": 1}

blockchain.subscribe_blocks

Initializes a subscription to new incoming blocks. Once a subscription is established, darkfid will send JSON-RPC notifications of new incoming blocks to the subscriber.
^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.subscribe_blocks", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "method": "blockchain.subscribe_blocks", "params": [`blockinfo`]}

blockchain.subscribe_txs

Initializes a subscription to new incoming transactions. Once a subscription is established, darkfid will send JSON-RPC notifications of new incoming transactions to the subscriber.
^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.subscribe_txs", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "method": "blockchain.subscribe_txs", "params": [`tx_hash`]}

blockchain.subscribe_proposals

Initializes a subscription to new incoming proposals. Once a subscription is established, darkfid will send JSON-RPC notifications of new incoming proposals to the subscriber.
^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.subscribe_proposals", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "method": "blockchain.subscribe_proposals", "params": [`blockinfo`]}

blockchain.lookup_zkas

Performs a lookup of zkas bincodes for a given contract ID and returns all of them, including their namespace.

Params:

• array[0]: base58-encoded contract ID string

Returns:

• array[n]: Pairs of: zkas_namespace string, serialized ZkBinary object
  ^[src]

--> {"jsonrpc": "2.0", "method": "blockchain.lookup_zkas", "params": ["6Ef42L1KLZXBoxBuCDto7coi9DA2D2SRtegNqNU4sd74"], "id": 1}
<-- {"jsonrpc": "2.0", "result": [["Foo", "ABCD..."], ["Bar", "EFGH..."]], "id": 1}

merge_mining_get_chain_id

Returns the chain_id used for merge mining. A 32-byte hash of the genesis block.
^[src]

--> {"jsonrpc": "2.0", "method": "merge_mining_get_chain_id", "params": [], "id": 0}
<-- {"jsonrpc": "2.0", "result": {"chain_id": 02f8...7863"}, "id": 0}

tx methods

• tx.simulate
• tx.broadcast
• tx.pending
• tx.clean_pending

tx.simulate

Simulate a network state transition with the given transaction. Returns true if the transaction is valid, otherwise, a corresponding error.
^[src]

--> {"jsonrpc": "2.0", "method": "tx.simulate", "params": ["base64encodedTX"], "id": 1}
<-- {"jsonrpc": "2.0", "result": true, "id": 1}

tx.broadcast

Broadcast a given transaction to the P2P network. The function will first simulate the state transition in order to see if the transaction is actually valid, and in turn it will return an error if this is the case. Otherwise, a transaction ID will be returned.
^[src]

--> {"jsonrpc": "2.0", "method": "tx.broadcast", "params": ["base64encodedTX"], "id": 1}
<-- {"jsonrpc": "2.0", "result": "txID...", "id": 1}

tx.pending

Queries the node pending transactions store to retrieve all transactions. Returns a vector of hex-encoded transaction hashes.
^[src]

--> {"jsonrpc": "2.0", "method": "tx.pending", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "result": "[TxHash,...]", "id": 1}

tx.clean_pending

Queries the node pending transactions store to remove all transactions. Returns a vector of hex-encoded transaction hashes.
^[src]

--> {"jsonrpc": "2.0", "method": "tx.clean_pending", "params": [], "id": 1}
<-- {"jsonrpc": "2.0", "result": "[TxHash,...]", "id": 1}

Anonymous nodes

This section provides two examples, one for hosting anonymous nodes using Tor, and the other one for making anonymous outbound connections with peers using Nym.

Hosting anonymous nodes

To connect to Tor, we use Arti. This is an experimental project with incomplete security features. See Arti's roadmap for more information.

Using Tor, we can host anonymous nodes as Tor hidden services. To do this, we need to set up our Tor daemon and create a hidden service. The following instructions should work on any Linux system.

1. Install Tor

Tor can usually be installed with your package manager. For example on an apt based system we can run:

# apt install tor

This will install it. Now in /etc/tor/torrc we can set up the hidden service. For hosting an anonymous ircd node, set up the following lines in the file:

HiddenServiceDir /var/lib/tor/darkfi_ircd
HiddenServicePort 25551 127.0.0.1:25551

Then restart Tor:

# /etc/init.d/tor restart

You can grab the hostname of your hidden service from the directory:

# cat /var/lib/tor/darkfi_ircd/hostname

For example purposes, let's assume it's jamie3vkiwibfiwucd6vxijskbhpjdyajmzeor4mc4i7yopvpo4p7cyd.onion.

2. Setup ircd

After compiling ircd, run it once to spawn the config file. Then edit it to contain the following:

inbound = ["tcp://127.0.0.1:25551"]
external_addr = ["tor://jamie3vkiwibfiwucd6vxijskbhpjdyajmzeor4mc4i7yopvpo4p7cyd.onion:25551"]

Now when you start ircd, the hidden service will be announced as a peer and people will be able to connect to it when they discover you as a peer.

These instructions are also applicable to other nodes in the DarkFi ecosystem, e.g. darkfid.

Anonymous outbound connection

Using Nym's mixnet to anonymously connect to other peers in Darkfi network as Nym offers network-level privacy.
An outbound connection with peers can be done anonymously using Nym, we will be proxying our packets through SOCKS5 Client to mixnet to Network Requester to other peers and back.
The following instructions should work on any Linux system.

1. Download

Nym binaries can be downloaded from Nym releases or pre-built for Ubuntu 20.04 x86-64 from nymtech website.
Download SOCKS5 Client and Network Requester.

2. Initialize

Network Requester makes the requests on your behalf, it is recommended to run your own on a server, however for the sake of example and simplicity everything is run locally.
We'll start by initializng the Network Requester:

% ./nym-network-requester init --id nettestnode

This will print some information in the terminal, what we want is the client address, for example it could be something like this:

The address of this client is: 8hUvtEyZK8umsdxxPS2BizQhEDmbNeXEPBZLgscE57Zh.5P2bWn6WybVL8QgoPEUHf6h2zXktmwrWaqaucEBZy7Vb@5vC8spDvw5VDQ8Zvd9fVvBhbUDv9jABR4cXzd4Kh5vz

Then we'll use that address as provider for SOCKS5 Client initialization:

% ./nym-socks5-client init --use-reply-surbs true --id sockstest --provider 8hUvtEyZK8umsdxxPS2BizQhEDmbNeXEPBZLgscE57Zh.5P2bWn6WybVL8QgoPEUHf6h2zXktmwrWaqaucEBZy7Vb@5vC8spDvw5VDQ8Zvd9fVvBhbUDv9jABR4cXzd4Kh5vz

We also set --use-reply-surbs flag to true, this will enable anonymous sender tag for communication with the service provider, but it will make the actual communication slower.

3. Run

Now we can run Network Requester and then SOCKS5 Client:

% ./nym-network-requester run --id nettestnode

Then in another terminal run:

% ./nym-socks5-client run --id sockstest

Adding a new domain/address to allowed.list while nym-network-requester is running you must restart it to pick up the new list.

Both of these binaries have to be running when setting up a node.

Currently connecting to other nodes might not be as dynamic as you'd think, there are two things we can do here:

1. Network Requester as open proxy:

you only need to run it like:

% ./nym-network-requester run --id nettestnode --open-proxy

This makes the whitelist not needed anymore, meaning you don't need to worry about adding peers to allowed.list anymore, but don't share the address of the Network Requester while running as open proxy randomly.

2. whitelisted addresses approach, here's how it works:

• Initialize nym-network-requester
• Initialize nym-socks5-client
• Add known peers' domains/addresses to ~/.nym/service-providers/network-requester/allowed.list
• Run nym-network-requester
• Run nym-socks5-client
• Edit Darkfi node's config file (provided in the next section) so you can connect to peers manually, or through seed.

Note that for peer discovery you'll have to whitelist some known peers and the seed itself.

4. Setup ircd

After compiling ircd, run it once to spawn the config file. Then edit it to contain the following:

# manually
## P2P net settings
[net]
outbound_connections=0
peers = ["nym://some.whitelisted.domain:25552", "nym://someother.whitelisted.domain:25556"]
outbound_transports = ["nym"]

# automatically
## P2P net settings
[net]
outbound_connections=8
seeds = ["nym://some.whitelisted.seed:25551", "tcp://someother.whitelisted.seed:25551"]
outbound_transports = ["nym"]

The most important part that could easily be forgotten is: outbound_transports = ["nym"]

Now when you start ircd, you will be able to discover or connect directly to peers and your traffic will be routed through the mixnet.

These instructions are also applicable to other nodes in the DarkFi ecosystem, e.g. darkfid.

Discrete Fast Fourier Transform

Available code files:

• fft2.sage: implementation using vandermonde matrices illustrating the theory section below.
• fft3.sage: simple example with $n=4$ showing 3 steps of the algorithm.
• fft4.sage: illustrates the full working algorithm.

Theory

$$f(x)g(x)\in {\mathbb{F}}_{<2n}[x]$$ $$fg=\sum _{i+j<2n-2}{a}_i{b}_j{x}^{i+j}$$ Complexity: $O(n^2)$

Suppose $\omega \in \mathbb{F}$ is an nth root of unity.

Recall: if $\mathbb{F}={\mathbb{F}}_{p^k}$ then $\exists N:{\mathbb{F}}_{p^N}$ contains all nth roots of unity.

$${\text{DFT}}_{\omega }:{\mathbb{F}}^n\to {\mathbb{F}}^n$$ $${\text{DFT}}_{\omega }(f)=(f({\omega }^0),f({\omega }^1),\dots ,f({\omega }^{n-1}))$$

$$V_{\omega }=\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }^1& {\omega }^2& \cdots & {\omega }^{n-1}\\ 1& {\omega }^2& {\omega }^4& \cdots & {\omega }^{2(n-1)}\\ ⋮& & & & \\ 1& {\omega }^{n-1}& {\omega }^{2(n-1)}& \cdots & {\omega }^{(n-1{)}^2}\end{array}\right)$$

$${\text{DFT}}_{\omega }(f)=V_{\omega }\cdot f^T$$ since vandermonde multiplication is simply evaluation of a polynomial.

Lemma: $V_{\omega }^{-1}=\frac{1}{n}{V}_{{\omega }^{-1}}$

Use $1+\omega +\cdots +{\omega }^{n-1}$ and compute $V_{\omega }{V}_{{\omega }^{-1}}$

Corollary: ${\text{DFT}}_{\omega }$ is invertible.

Definitions

1. Convolution $f\ast g=fg\mathrm{mod}(x^n-1)$
2. Pointwise product $$(a_0,\dots ,a_{n-1})\cdot (b_0,\dots ,b_{n-1})=(a_0{b}_0,\dots ,a_{n-1}{b}_{n-1})\in {\mathbb{F}}^n\to {\mathbb{F}}_{<n}[x]$$

Theorem: ${\text{DFT}}_{\omega }(f\ast g)={\text{DFT}}_{\omega }(f)\cdot {\text{DFT}}_{\omega }(g)$

$$fg=q^{\prime }(x^n-1)+f\ast g$$ $$\Rightarrow f\ast g=fg+q(x^n-1)$$ $$\mathrm{deg}fg\le 2n-2$$

$$\begin{array}{rl}(f\ast g)({\omega }^i)& =f({\omega }^i)g({\omega }^i)+q({\omega }^i)({\omega }^{in}-1)\\ & =f({\omega }^i)g({\omega }^i)\end{array}$$